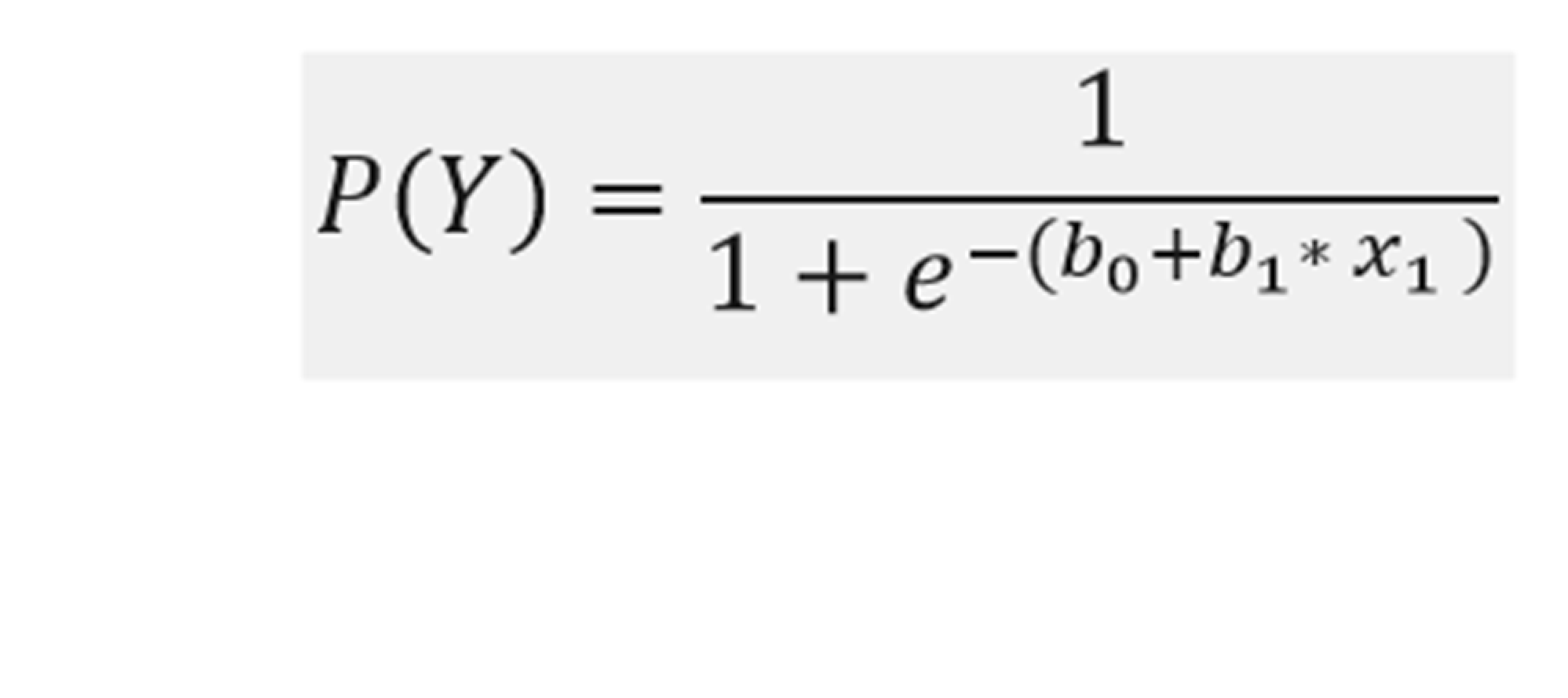Binárna logistická regresia je špecifický typ regresnej analýzy, pri ktorej je závislá premenná v nominálnej forme a nadobúda dve hodnoty, zvyčajne kódované ako 0 alebo 1. Nezávislá premenná môže byť ordinálna aj intervalová. Aby sme dokázali určiť, či nezávislá premenná spôsobuje, že závislá premenná nadobudne jeden alebo druhý stav (sa stane nulou alebo jednotkou), potom musíme pracovať s pravdepodobnosťami. Preto aj vzorec na vzťah medzi závislou premennou (Y) a nezávislou (X) je odlišný od vzorca, ktorý sa používa pri lineárnej regresii. Matematicky vyjadrený vzťah medzi premennými je nasledovný:
Kde: e – je základ prirodzeného algoritmu.
Ostatné premenné v rovnici sú rovnaké ako pri lineárnej regresii, ktoré opisujeme v inom okne web stránky.
1 úloha: V databázovom súbore Príklad č. 7 s názvom Canvas metódy a startup.sav sú uvedené opisné charakteristiky 200 podnikateľských zámerov, kde začínajúci podnikatelia žiadali finančné prostriedky od nezávislých investorov na rozvoj ich podnikateľského zámeru. Pri prvotnom hodnotení špecializovaní poradcovia hneď vylúčili 116 podnikateľských zámerov ako nekvalitných a 84 akceptovali na ďalšie hodnotenie. Podnikateľský zámer bol teda odmietnutý (kódovaný ako 0) alebo akceptovaný (kódovaný 1). Canvas metóda je podnikateľský postup, pomocou ktorého sa opisuje podnikateľský zámer v konkrétnych kategóriách. Hodnotia sa ako dobre sú definovaný zákazníci, ako sa budú získavať príjmy, aké zdroje budú potrebné a mnohé iné charakteristiky, ktoré sumárne opisujú podnikateľský zámer. Jednou z kategórií Canvas sú segmenty zákazníkov (Customer Segments), ktoré boli merané na škále od skóre 0 (nemá definovaných zákazníkov) po skóre 10 (zákazníci sú podrobne, jednoznačne a dôkladne definovaní). Segmenty zákazníkov môžu byť opísané veľmi dôkladne a podrobne a preto pri hodnotení dostane vysoké skóre, alebo môže byť opísaný nedostatočne a povrchne a skóre je potom nižšie.
V našej analýze nás zaujíma či tie podnikateľské zámery, kde boli opísané Segmenty zákazníkov dôkladne a podrobne (mali lepšie definované segmenty zákazníkov a teda vyššie skóre) mali vyššiu pravdepodobnosť byť akceptované oproti tým, ktoré mali skóre v Segmentoch zákazníkov nízke.
Riešenie:
V našom príklade je závislá premenná dichotomická (akceptovaný verzus odmietnutý) a nezávislá premenná (skóre v segmentoch zákazníkov) je škálová (môže nadobúdať hodnoty 0 až 10). Zvolíme preto binárnu logistickú regresiu.
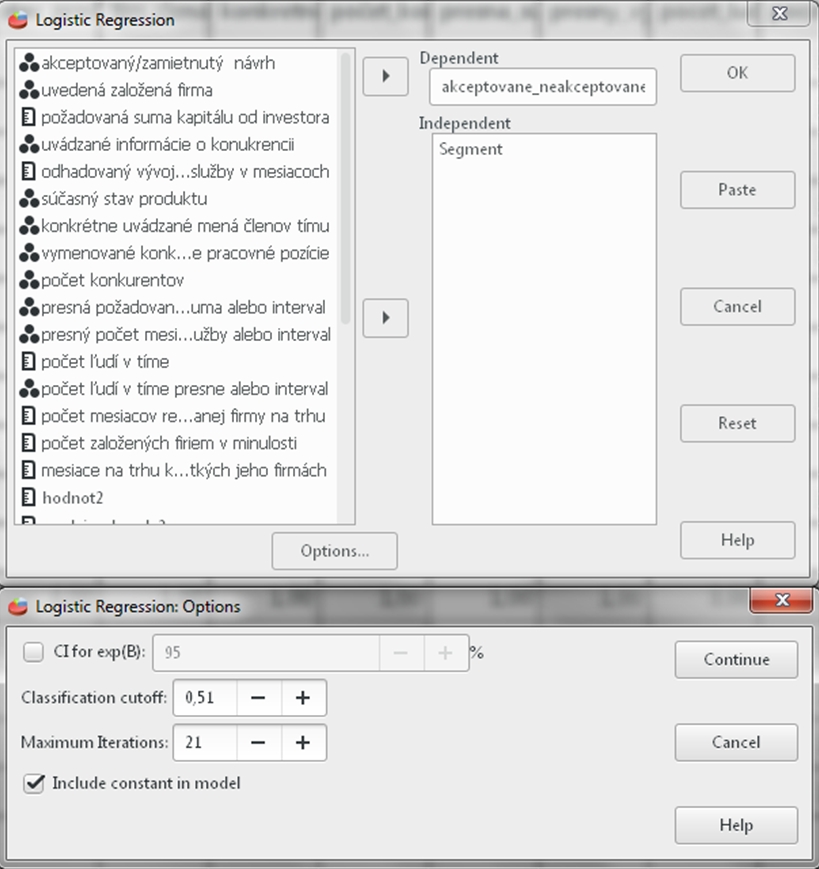
Otvoríme si príklad č. 7 Canvas metódy a startup. Následne klikneme na Analyzovať (Analyze) vyberieme si Regresiu (Regression) a z dvoch dostupných možností si vyberieme Binárnu Logistickú (Binary Logistics). V sprievodcovi binárnou logistickou regresiou musíme si definovať závislú premennú. V našom prípade je to premenná akceptovane_neakceptovane. Nezávislá premenná – tá ktorá ovplyvňuje závislú premennú je Segementy zákazníkov, označená ako Segment. Ďalej klikneme na Možnosti (Options) a v sprievodcovi zaškrtneme nastavenia Intervalov spoľahlivosti (confidence intervals). Softvér PSPP v niektorých prípadoch požaduje iné nastavenia iterácií, než je predvolené a bez tejto zmeny nevypočíta výsledok. Preto počet iterácií výpočtu zvýšime na 21 (Maximum iterations), a Clasification cutoff zvýšimi na 0,51 a zaškrtneme políčko Konštanta v modeli (Include constant in model). Zvýšenie o jednu jednotku v oboch hore uvedených príkladoch sme zaklikli preto, aby nás softvér pustil ďalej a vypočítal výsledok. Klikneme na Pokračovať (Continue) následne OK.
Obr. 1 Sprievodca binárnou logistickou regresiou
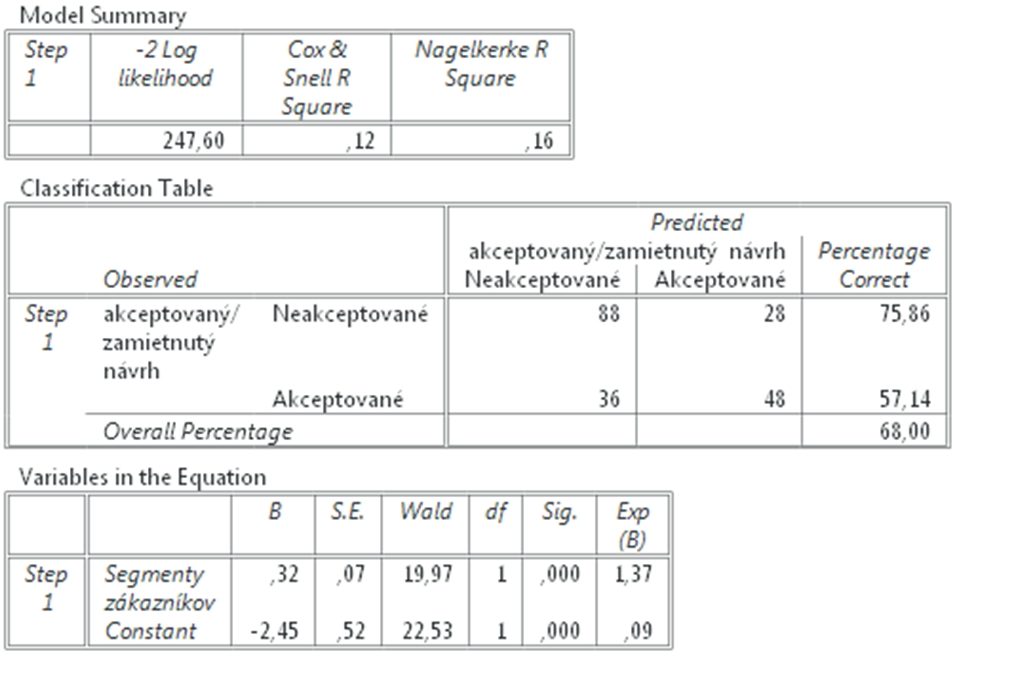
Výsledky: Výsledkom je päť tabuliek a my budeme interpretovať údaje z posledných troch.
Obr. 2 Výsledok binárnej logistickej regresie, posledné 3 tabuľky.
Tretia tabuľka je sumárny model (Model Summary), ktorá uvádza koľko variancie model vysvetľuje. Výsledok je vypočítaný dvoma metódami, kde Cox & Snell R Square = 0,12 a Nagelkerke R Square = 0,16, čo znamená že model vysvetľuje podľa Cox & Snell 12% variability a podľa Nagelkerke 16% variability.
Posledná, piata tabuľka je najdôležitejšia. Vysvetlíme si čo znamenajú jednotlivé výsledky. Stĺpec Wald nám hovorí či b koeficient pre prediktor je štatisticky významne odlišný od nuly. V našom prípade teda či predpovedá výsledok výberu. Vidíme, že Wald(ovo) z rovné 19,97 a p < 0,001. Hladina významnosti v našich výsledkoch je oveľa nižšie než všeobecne akceptovaná podmienka p <0,05.
Exp(B) je exponenciálne B, ktoré vyjadruje zvýšenie pomeru šancí (odds ratio) výskytu udalosti pri zvýšení hodnoty prediktora o jednotku. Pomer šancí (odds ratio) Field (2013, str. 880) definuje ako: „pomer šancí výskytu udalosti v jednej skupine v porovnaní s výskytom udalosti v druhej skupine.“ Field uvádza príklad, kde šanca výskytu určitej udalosti v jednej skupine je napríklad 4 a v druhej skupine je napríklad len 0,25, tak vzájomný pomer je 4/0,25 = 16. Ak je je exponenciálne B Exp(B) rovné 1, pomer šancí v jednej aj v druhej je rovnaký a potom zmeny prediktora nemajú žiaden vplyv. Ak je väčšie ako 1, potom zvyšovaním prediktora rastú šance na výskyt udalosti. Výsledok v našom prípade je Exp(B) = 1,37 teda ak zýšime hodnotu v nezávislej premennej o jednu 1 potom vzrastie pomer šancí byť akceptovaný na 1,37.
Interpretácia:
Dosiahnuté skóre v Segmentoch zákazníkov je štatisticky významný prediktorom pre akceptáciu podnikateľského plánu investormi, Wald(ovo) Z je 19,97 a p < 0,001, exponenciálne B (Exp. B) = 1,37. Model vysvetľuje R squared = 0,16 variability (Nagelkerke).
Spracoval Róbert Hanák, 5 Júl 2015