Dátové súbory

V nasledujúcich odkazoch je uvedených 7 dátových súborov na stiahnutie, ktoré sú založené na skutočne zozbieraných dátach v rámci Slovenskej republiky. Tieto príklady opakovane uvádzame aj pri jednotlivých konkrétnych príkladoch v časti štatistická analýza. Všetky súbory sú zozipované a tak ich treba rozbaliť.

Príklady vytvoril a spracoval Róbert Hanák, august 2015

Zoznam literatúry

Na web stránke sa užívateľ často stretol s odkazmi na literatúru. V prípade záujmu čitateľa uvádzame nasledovné zoznamy:

V prvom zozname je všetka použitá literatúra
V druhej časti je literatúra, ktorú odporúčam záujemcom o samo štúdium

A: Použitá literatúra:

Acton, C., Miller, R. 2009. SPSS for social scientists. New York, Palgrave Macmillan, ISBN 978-0-230-20993-0
Anýžová, P. (2014). Srovnatelnost Schwartzovy hodnotové škály v mezinárodních datech. Sociologický časopis/Czech Sociological Review, (04), 547-580.
Betsch, C. (2004). „Präferenz für Intuition und Deliberation (PID): Inventar zur Erfassung von affekt- und kognitionsbasiertem Entscheiden“. Zeitschrift fur differentielle und diagnostische psychologie, Volume 25, No. 4, 179–197.
Brož, M., Bezvoda, V. Microsoft Excel Vzorce, funkce, výpočty. Computer Press, Brno. ISBN 80-251-1088-5
Budíková, M., Králová, M., Maroš, B. Prúvodce základními statistickými medotami. Grada publishing, a.s., Praha, ISBN 978-80-247-3243-5
Černík, V., & Viceník, J. (2011). Úvod do metodológie spoločenských vied. Bratislava: Iris.
Chajdiak, J. (2005). Štatistické úlohy a ich riešenie v Exceli. Statis.
Chajdiak, J. (2009). Štatistika v exceli 2007. Bratislava, Statis, 151-156.
Chajdiak, J. (2013). Analýza dotazníkových údajov, Statis.
Disman, M. 2002 . Jak se vyrábí sociologická znalost. Praha, Karolinum. ISBN 80 – 246 -0139-7
Field, A. (2013). Discovering statistics using IBM SPSS statistics. Sage.
Field, A., & hole, G. J. (2002). How to design and report experiments. Sage.
Halama, P. (2005). Princípy psychologickej diagnostiky. Typy Universitatis Tyrnaviensis.
Hanák (2014) Are deliberative people more consistent in decision making? In Advances in cross-cultural decision making / recenzenti: Abbe, A., Appleget, J. – [s.l.] : AHFE Conference, 2014. – ISBN 978-1-4951-2095-4. – pp. 43-52, [1,1 AH].
Hanák, R. (2014) Rozhodovanie expertov v personálnom manažmente. Bratislava: Vydavateľstvo EKONÓM, ISBN 978-80-225-3920-3
Hanák, R. (2014) Rozhodovanie expertov v personálnom manažmente. Bratislava : EKONÓM, ISBN 978-80-225-3920-3
Hanák, R., Sirota, M., & Juanchich, M. (2013). Experts use compensatory strategies more often than novices in hiring decisions. Studia Psychologica, 55(4), 251.
Hendl, J. (2009) Přehled statistických metod. Praha, Portál. ISBN 978-80-7367-482-3
Hendl, J. (2014) Statistika v aplikacích. Portál, Praha. ISBN 978-80-262-0700-9
Hendl, J. (2016) Kvalitativní výzkum: základní metody a aplikace. Portál. Praha, ISBN 978-80-262-0982-9
Hindls, R., Hronová, S., Seger, J., & Fischer, J. (2007). Statistika pro ekonomy. Professional publishing.
Juszczyk, S. (2003). Metodológia empirických výskumov v spoločenských vedách. Iris.
Kokles, M. – romanová, A. 2007. Informačný systém podniku. Bratislava: Ekonóm, 2007. 183 s. ISBN 978-80-225-2286-1.
Mareš, P., Rabušic, L., & Soukup, P. (2015). Analýza sociálněvědních dat (nejen) v SPSS. Masarykova univerzita.
Martin, P., & Bateson, P. P. G. (2009). Úvod do teorie a metodologie měření chování. Portál.
Meloun, M., & Militký, J. (2002). Kompendium statistického zpracování dat: metody a řešené úlohy včetně CD. Academia.
Meloun, M., & Militký, J. (2002). Kompendium statistického zpracování dat: metody a řešené úlohy včetně CD. Academia.
Meloun, M., Militký, J., & Hill, M. (2012). Statistická analýza vícerozměrných dat v příkladech. Academia.
Mikusková, E. B., Hanák, R., & Cavojová, V. (2015). Appropriateness of Two Inventories Measuring Intuition (the Pid and the Rei) for Slovak Population. Studia Psychologica, 57(1), 63.
Neubauer, J., Sedlačík, M., & Kříž, O. (2012). Základy statistiky: Aplikace v technických a ekonomických oborech. Grada.
Ochrana, F. (2013). Metodologie sociálních věd. Karolinum Press.
Ondrejkovič, P., & Majerčíková, J. (2012). Vysvetlenie, porozumenie a interpretácia v spoločenskovednom výskume.
Pacáková, V. a kol. (2003): Štatistika pre ekonómov. Bratislava: Iura Edition. ISBN 80-89047-74-2
Pacáková, V. a kol. (2009): Štatistické metódy pre ekonómov. Bratislava: Iura Edition. ISBN 987-80-8078-284-9
Pacáková, V. a kol. (2015): Štatistická indukcia pre ekonómov a manažérov. Wolters Kluwer. ISBN: 9788081680816
Pelikán, J. Základy empirického výzkumu pedagogických jevů. Praha: Karolinum, 1998. 270 s. ISBN 80-7184-569-8.
Ptáček, R, Raboch J. (2010) Určení rozsahu souboru a power analýza v psychiatrickém výzkumu. Česká a Slovenská Psychiatrie 106 (1) 33- 41
Punch, K. (2008). Úspěšný návrh výzkumu. Praha: Portál. ISBN 978-80-7367-468-7.
Řehák, J., Brom, O. (2015) SPSS – Praktická analýza dat. Computer Press, Brno, ISBN 978-80-251-4609-5
Rimančík, M. (2007) Štatistika pre prax. ISBN 978-80-969813-1-1
Ritomský, A. (1994) SPSS pre Windows. C.T.S Bratislava, ISBN 80-967050-1-6
Ritomský, A. (1999). Deskripcia dát pomocou SPSS: sondy do súčasnej rodiny a domácnosti. Medzinárodné stredisko pre štúdium rodiny.
Sawilowsky, S (2009). „New effect size rules of thumb.“. Journal of Modern Applied Statistical Methods. 8 (2): 467–474
Sollár, T., & Ritomský, A. (2002). Aplikácie štatistiky v sociálnom výskume. Univerzita Konštantína Filozofa.
Šoltés, Erik, (2015): Štatistické metódy pre ekonómov. Bratislava: Wolters Kluwer. ISBN: 9788081682346
Soukup, P. (2013). Věcná významnost výsledků a její možnosti měření. Data a výzkum – SDA Info, Vol. 7, No. 2: 125-148.
Terek, M. (2007). Analýza rozhodovania. Iura Edition.
Terek, M. (2013). Interpretácia štatistiky a dát. ISBN 978-80-8143-100-5
Terek, M. (2013). Interpretácia štatistiky a dát. Podporný učebný materiál. Equilibria. ISBN 978-80-8143-101-2
Terek, M., Horníková, A., Labudová, V. (2010): Hĺbková analýza údajov, Wolters Kluwer (Iura Edition), ISBN: 9788080783365
Walker, I. A. N. Výzkumné metody a statistika. Praha: Grada, 2013 (pp. 37-40). ISBN 978-80-247-3920-5.

B: Opis vybraných konkrétnych kníh:

Z hore uvedených kníh sú niektoré napísané pre pokročilého čitateľa, iné sú skôr teoreticky orientované, ďalšie obsahujú len také úvodné uvedenie do problematiky a preto som spracoval nasledovný zoznam, ktorý môže niektorým užívateľom uľahčiť hľadanie. Tento zoznam je čisto subjektívny a som presvedčený to tom, že iní užívatelia by si vytvorili vlastné zoznamy s inými knihami. Do zoznamu som sa snažil začleniť všetky štatistické knihy, ktoré som našiel v internetovom obchode Martinus.sk dostupné v roku 2016. Určite som však niektoré nenašiel alebo som sa k nim nedostal, nech mi autori kníh prepáčia, ak som sa k ich knihe nedostal a nepoznám ju.

Ak viete čítať po anglicky a ste úplný začiatočník a máte záujem pochopiť podstatu jednotlivých štatistických testov a súčasne sa chcete v softvéri SPSS naučiť ako test realizovať i interpretovať výsledky, potom odporúčam knihy od Andyho Fielda. Ak si máte prečítať jedinú štatistickú knihu, z ktorej sa chcete všetko naučiť, tak si subjektívne myslím že by to mohla byť táto: Discovering statistics using IBM SPSS statistics.

Ak chcete realizovať štatistické testy pomocou programu MS Excel, tak odporúčam knihy od Jozefa Chajdiaka ako aj od Broža a Bezvodu. V tomto prípade treba počítať s obmedzením programu MS Excel, ktorý ponúka len určitý počet štatistických metód a testov oproti rozsiahlym a špecializovaným štatistickým softvérom.

Ľahko čitateľná, kvalitná a súčasne s praktickými príkladmi riešenia úloh v SPSS je kniha od kolektívu Mareša, Rabušica a Soukupa: Analýza sociálněvědních dat (nejen) v SPSS.

Na hlbšie pochopenie metód, teórie a matematického základu odporúčam knihy od Hendla, Tereka a Pacákovej, Melouna & Militkého. Tieto obsahujú aj konkrétne vzorce, matematické vzťahy, definície a exaktný matematický aparát.

Ostatné knihy uvedené v zozname literatúry sú zvyčajne špecializované na konkrétnu oblasť, čo je zvyčajne priamo uvedené aj v názve knihy.

Lineárna regresná analýza

Úvod
Pri regresnej analýze skúmame vzťah medzi dvoma, prípadne medzi viacerými premennými. Predpokladáme, že 1 premenná závisí od druhej premennej, ktorá ju ovplyvňuje. Tých premenných, ktoré ovplyvňujú môže byť aj viacero, nielen jedna. Premenná, ktorá závisí od inej alebo od viacerých sa nazýva závislá, po anglicky dependend variable (DV, v regresnej rovnici sa označuje Y). Tá premenná, alebo ak ich je viac, tak tie premenné, ktoré ju ovplyvňujú sa nazývajú nezávislé premenné, independent variable (IV, v regresnej rovnici označené X) alebo aj prediktor. Ak je medzi premennými lineárny vzťah, potom nám regresná analýza umožní presne matematicky vyjadriť tento vzťah. Napr. ak zvýšime premennú X (nezávislú premennú, IV) o 1 jednotku, tak sa druhá premenná (závislá, DV) zvýši o 1,25. Matematický vzťah premenných v regresnej rovnici sa vyjadruje nasledovne:
Pre 1 nezávislú premennú:
Y = b0+ b1* X + e
Pre viac nezávislých premenných:
Y = b0+ b1* x1 + b2* x2 + … bn* xn + e
kde: Y – je závislá premenná, X je nezávislá premenná(é), b0 je bod, kde regresná priamka pretína osu Y, b1 je regresný koeficient, ktorý určuje smer priamky, e je chyba merania.

Zadanie:

Príklad č. 2 Študenti body a pamäť
Študenti boli požiadaní, aby posúdili v limitovanom čase do 3 minúť podnikateľský plán začínajúceho podniku, ktorý bol opísaný 25 charakteristikami ako napríklad súčasná konkurencia, ziskovosť, vzhľad produktu, cena a ostatné. Študenti videli len názov ale ich obsah nevideli, a museli vždy kliknúť na políčko napr. ziskovosť, ak chceli vedieť aká konkrétna je ziskovosť v tomto podnikateľskom pláne. Študenti zároveň vyplnili dotazník PID, ktorý meria preferenciu k intuícii a uvažovaniu – deliberácii pri rozhodovaní.
Vypočítajte či má preferencia k intuícii vplyv na počet otvorených podnikateľských charakteristík pri posudzovaní podnikateľského plánu.
Predpokladáme, že študenti, ktorí sa v rozhodovaní spoliehajú na intuíciu, dokážu prijímať rozhodnutia s menším počtom informácií než rozvažujúci študenti, ktorí viac hĺbajú nad problémom (Betsch, 2004). Teda čím viac bude študent intuitívnejší, tým menej informácií bude potrebovať pri rozhodovaní a otvorí si menej charakteristík podnikateľského plánu.
Hypotézy sme si stanovili nasledovne:
H1: Dosiahnuté skóre v škále intuícia v dotazníku PID je štatisticky významným prediktorom počtu otvorených podnikateľských charakteristík pri posudzovaní podnikateľského plánu.
H0: Dosiahnuté skóre v škále intuícia v dotazníku PID nie je štatisticky významným prediktorom počtu otvorených podnikateľských charakteristík pri posudzovaní podnikateľského plánu.

Riešenie:
Na riešenie použijeme lineárnu regresnú analýzu, ktorej postup v programe PSPP je nasledovný. Klikneme Analyzovať (Analyze) potom na Regresia (Regression) a vyberieme Lineárna regresia (Linear). Ďalej klikneme na Štatistiku (Statistics) a zaškrtneme všetky políčka. Ich obsah si vysvetlíme v časti výsledky.
Pri regresii musíme správne nastaviť jednotlivé parametre analýzy ako aj premenné a ich miesto v analýze. V dialógovom okne určíme najprv závislú (Dependent variable – DV) a nezávislú premennú (Independent variable – IV). V našom prípade nás zaujíma ako preferencia k intuícii ovplyvňuje počet otvorených podnikateľských charakteristík pri posudzovaní podnikateľského plánu. Teda preferencia k intuícii uvedená ako: PID_intu bude nezávislá premenná (Independent variable) a počet otvorených podnikateľských charakteristík uvedený ako: Počet_otv_I bude závislá premenná (Dependent variable). Počet otvorených závisí od intuície študenta. Ďalej v dialógovom okne v ľavej časti dole Štatistika(Statistics) zaškrtneme všetky políčka.

Obr. 1. Sprievodca regresnou analýzou

Výsledky:
Program PSPP vytvorí štyri tabuľky, ktoré si podrobne opíšeme.

Obr. 2. Výsledok lineárnej regresie

Prvá tabuľka s názvom Sumarizácia Modelu (Model Summary) opisuje regresný model. Význam jednotlivých koeficientov je nasledovný:
R je korelačný koeficient medzi počtom otvorených podnikateľských charakteristík a škálou intuície. V našom prípade je 0,09, čo je hodnota blízka nule. To znamená že medzi našimi premennými je len veľmi slabý vzťah.
R Square je koeficient determinácie. Je druhou mocninou korelačného R a vysvetľuje koľko percent variability závislej premennej Y – Počet otvorených podnikateľských charakteristík ovplyvňuje nezávislá premenná X – škála intuície. V našom prípade vidíme, že hodnota je veľmi nízka, rovná 0,01, teda 1%. Inými slovami, to ako intuitívni študenti sú, ovplyvnilo len 1 % z toho, koľko podnikateľských charakteristík si otvorili. 99% ovplyvňujú všetky ostatné faktory ako napríklad skúsenosť, sebaistota a iné.
Tabuľka ANOVA udáva ako dobre regresný model opisuje dáta. Posledné dva stĺpce uvádzajú hodnotu F = 0,6 a p = 0,44, čo je oveľa viac než akceptovaná hladina štatistickej významnosti p < 0,05.
V poslednej tabuľke sú uvedené koeficienty regresnej rovnice. V stĺpci B, Neštandardizované koeficienty (Unstandardized coefficients) je hodnota b0 = 14,97 a b1 = – 0,1. Z týchto koeficientov vieme zostaviť regresnú rovnicu, ktorá bude vyzerať nasledovne.
Y = 14,97 – 0,1* X, teda:
Počet otvorených podnikateľských charakteristík = 14,97 – 0,1* Skóre v škále intuícia (PID)
Ďalej je dôležité všimnúť si štandardizovaný koeficient (Standardized Coefficient) Beta, pre PID dotazník škála intuície, ktorý je 0,09 na hladine významnosti p = 0,44. Tá je vyššia než podmienka na prijatie hypotézy H1, ktorá je p < 0,05. V prípade, že máme len jednu nezávislú premennú, čo je aj náš prípad, potom je tento koeficient zhodný s korelačným koeficientom R v prvej tabuľke.
Intervaly spoľahlivosti pre B (95% Confidence Interval for B) sú CI [-0,37, 0,16] nám hovoria o tom kde sa bude pravdepodobne nachádzať hodnota hľadaného parametra. V rámci nášho intervalu sa nachádza 0, to znamená, že hľadaný parameter môže byť nulový.
Na základe hore uvedených výsledkov zamietame hypotézu H1 a prijímame hypotézu H0.
Poznámka:
V tomto príklade sme postupovali ako odporúčajú vedecké postupy, teda že mali sme určité teoretické predpoklady, podľa nich sme si stanovili hypotézy, navrhli výskum, zozbierali dáta na záver sme ich otestovali. Výsledky jednoznačne preukázali, že lineárny regresný vzťah medzi premennými neexistuje a intuícia meraná dotazníkom PID vôbec neovplyvňuje počet otvorených podnikateľských charakteristík. U začiatočníkov mohlo vyvolať sklamanie, že sme nepotvrdili hypotézu H1, avšak naše výsledky sú z vedeckého hľadiska rovnako hodnotné ako keby sme hypotézu potvrdili.

Reportovanie výsledkov:
Dosiahnuté skóre v škále intuícia merané dotazníkom PID nepredikuje počet otvorených podnikateľských charakteristík F(1, 73) = 0,6, p = 0,44. Vzájomný vzťah medzi premennými je takmer nulový a regresný model vysvetľuje len minimum variancie v počte otvorených ponikateľských charakteristík, koeficient determinácie R sq = 0,01 .

Spracoval Róbert Hanák, 7 September 2015

O nás

Vitajte na vzdelávacej štatistickej webstránke.

Dvojvýberový t – test s rovnosťou rozptylov

Dvojvýberový t – test s rovnosťou rozptylov

Zadanie: Porovnajte celkové skóre v intuícii u mužov a u žien.

Riešenie: Muži a ženy sú dve nezávislé skupiny v súbore, teda jedna druhú neovplyvňujú. Preto použijeme t – test pre dva nezávislé výbery (Independent samples T test). Mužov máme v súbore kódovaných v stĺpci pohlavie ako 1 a ženy ako 2. Pri porovnávaní skupín odporúčam stanoviť si hypotézy, ktoré nám pomôžu lepšie si ujasniť skúmanú otázku a vnímať problém exaktnejšie.

Čítať ďalej→

Korelácia

Korelačná analýza

Dáta na korelačnú analýzu nájdete v súbore s názvom:

korelačná analýza

Korelačná analýza je analýza závislosti dvoch premenných. Pomocou nej zisťujeme, ak sa mení 1 premenná, či to ovplyvňuje druhú premennú. Priama korelačná závislosť znamená, že ak rastie jedna premenná, potom aj druhá rastie. Napríklad čím viac kalórií prímam bez pohybu, tým viac vážim. Nepriama korelačná závislosť znamená, že keď jedna premenná rastie, potom druhá klesá. Napríklad u obéznych ľudí, čím viac športujú, tým menej vážia.

Výsledkom korelačnej analýzy je koeficient r, ktorý nadobúda hodnoty v intervale od -1 do +1. Mínus 1 znamená absolútnu nepriamu lineárnu závislosť, 0 znamená žiadnu závislosť a 1 znamená absolútnu priamu lineárnu závislosť. Inými slovami: čím je korelačný koeficient bližšie k 0, tým je vzťah medzi skúmanými premennými slabší, resp. neexistujúci. Naopak čím je bližšie k 1 alebo k -1, tým je vzťah medzi premennými silnejší. V praxi však tieto koeficienty takmer nikdy nenadobúdajú tieto hraničné hodnoty, ale sa pohybujú niekde v intervale. Preto my musíme hodnoty interpretovať sami. Hodnoty koeficientu korelácie 0,8 až 1 (-0,8 až -1) sú považované zvlášť silné, teda medzi premennými existuje veľmi silná vzájomná závislosť. Hodnoty 0,4 až 0,8 (-0,4 až -0,8) sú stredne silné a od 0 do 0,4 (-0,4 až 0 ) sú považované za slabé.

Zadanie:

Vypočítajte vzájomnú koreláciu medzi subškálami dotazníka PID deliberáciou a intuíciou.

Riešenie:

V súbore klikneme na Analyzovať (Analyze)→ Korelácia dvoch premenných (Bivariate Corelation).

V dialógovom okne si vyberieme dve premenné z ktorých chceme počítať vzájomnú koreláciu. V našom prípade je to sumárne skóre PID deliberácia a sumárne skóre PID intuícia. Ak by sme chceli korelovať viac premenných, tak ich presunieme všetky a v tom prípade bude výstupom korelačná matica. V spodnej časti sú dve zaškrtávacie políčka. Označenie jednostranného testu (one-tailed) a dvojstranného testu (Two-tailed). Ponecháme prednastavenú hodnotu two-tailed. Ďalej sa v ľavom dolnom rohu nachádza možnosť zaškrtnúť Označenie signifikatných korelácií (Flag significant correlations). Túto možnosť zaškrtneme tiež. Kliknutím OK spustíme celú analýzu.

Obr. 1. Sprievodca koreláciou

Naše výsledky:

Obr. 2 Výsledky korelačnej analýzy

Ako vidíme v tabuľke jednotlivé škály dotazníka PID spolu korelujú len slabo r = 0,25, p < 0,001.

Reportovanie výsledkov:

Reportovanie našich výsledkov: Škála PID deliberácia koreluje r = 0,25, zo škálou PID intuícia na hladine významnosti p < 0,001.

Môžeme aj kratšie: Škála PID deliberácia koreluje r = 0,25, p < 0,001, zo škálou PID intuícia.

Príklady medzinárodného (anglického) reportovania výsledkov (nesúvisia s príkladom) :

The most useful was REI-R scale that correlated with three other measures: CRT (r=0.14, p<0.01), time preference (r=0.105, p<0.05), and risk preference (r=0.115, p<0.05). (Čavojová, Hanák, 2014).

Alebo:

As we stated earlier, measures of rational thinking showed only weak correlations among themselves (CRT correlating with a composite score for risk preference, r=0.09, p=0.04 and the jelly bean task, r=0.118, p=0.007; and time preference correlating with risk preference, r=0.24, p<0.001,and Wason´s task, r=0.12, p=0.005) (Čavojová, Hanák, 2014).

Spracoval Róbert Hanák, Január 2016

Opisná štatistika

Opisná štatistika

Dáta na počítanie opisnej štatistiky nájdete v súbore s názvom:

korelačná analýza

Pomocou základných štatistík ako priemer, smerodajná odchýlka a ostatné opisujeme súbor dát. Nakoľko pri akomkoľvek štatistickom skúmaní je zvykom uvádzať základné opisné štatistiky, je počítanie opisných štatistík časté. Pri publikovaní vedeckých článkov a príspevkov je vždy potrebné uvádzať priemer a smerodajnú odchýlku z našich dát, aby iní autori mohli eventuálne náš výskum zaradiť do metaanalýz. Zároveň sa opisné štatistiky vždy vyžadujú editormi vo vedeckých časopisoch alebo v iných vedeckých prácach.

Patria sem:

Priemer (Mean) je aritmetický priemer.

Smerodajná odchýlka (Standard deviaton) je štandardná smerodajná odchýlka.

Minimum (Minimum) je minimálna hodnota v súbore

Maximum (Maximum) je maximálna hodnota v súbore

Rozpätie (Range) je rozdiel medzi maximálnou a minimálnou hodnotou.

Suma (Sum) je súčet všetkých hodnôt v súbore

Štandardná chyba (Standard error) uvádza rozptýlenosť ostatných vypočítaných štatistík.

Rozptyl (Variance) je vyjadrením variability v súbore a smerodajná odchýlka je druhá odmocnina rozptylu. Čím máme v súbore dáta odlišnejšie od priemeru (moc veľké alebo moc malé), tým je rozptyl väčší.

Šikmosť (Skewness) Vyjadruje zošikmenie súboru, teda zjednodušene či prevažujú vysoké hodnoty alebo nízke hodnoty v súbore. Ak vyjde koeficient šikmosti nula, potom ide o symetrické rozdelenie. Ak je menší ako nula ide o vpravo zošikmené rozdelenie (viac väčších hodnôt a málo menších), ak je koeficient vyšší ako 0 ide o vľavo zošikmené rozdelenie (viac menších hodnôt a málo väčších).

Špicatosť (Kurtosis) Vyjadruje rozloženie dát v súbore. Ak je výsledok väčší ako 0 potom je to špicatejšie rozdelenie a ak je výsledok menší ako 0 potom je rozdelenie plochejšie. Špicaté rozdelenie prakticky znamená, že väčšina hodnôt v súbore je blízko priemeru. Plochejšie rozdelenie naopak znamená, že v súbore máme veľa nízkych aj vysokých hodnôt a nie sú blízko priemeru.

Zadanie:

Vypočítajte opisné štatistiky pre sumárnu škálu dotazníka PID deliberácia a intuícia. Tie sú v našom súbore uvedené ako posledné stĺpce vpravo a pod skratkami PID_del_total (PID škála deliberácia) a PID_In_total (PID škála intuícia).

Riešenie:

Klikneme Analyzovať (Analyze) → Opisná štatistika (Descriptives)

V ľavej časti okna sú uvedené všetky premenné v našom súbore. Vyberieme PID_del_total (PID škála deliberácia) a PID_In_total (PID škála intuícia) a presunieme ich do pravej časti s názvom Premenné (Variables) .

V dialógovom okne nám v pravej časti dole ponúka jednotlivé opisné štatistiky. Zaškrtávacím políčkom vyberiem tie, ktoré potrebujeme a následne klikneme ok a spustíme celú analýzu.

Obr. 1 Postup riešenia výpočtu opisných štatistík.

Výsledky:

Program PSPP vytvorí tabuľku s výsledkami. Dole na obrázku vidíme, že sme mali 872 prípadov a ani v jednom z nich nám nechýbali hodnoty.

Obr. 2. Výsledky riešenia opisnej štatistiky.

Interpretácia

V súbore sme mali veľkú vzorku, takže to nám dovoľuje robiť úsudky aj o celej populácii. Môžeme konštatovať, že respondenti vnímali seba samých viac deliberatívne (racionálnejšie), kde priemer M = 34,17 než intuitívne M = 30,7. Zároveň bola v jednotlivých odpovediach na otázky deliberatívnej škály väčšia variabilita o čom svedčí vyššia smerodajná odchýlka SD = 5,81 v porovnaní s intuitívnou škálou, kde SD = 5,05. Maximálnu hodnotu, ktorú mohol respondent dosiahnuť bolo 45 bodov a u obidvoch škál boli respondenti, ktorí túto hodnotu dosiahli. Čo sa týka minimálnej hodnoty, tak u škály deliberácia bola 9 bodov a u škály Intuícia 13 bodov. Špicatosť (Kurtosis) bola u škály intuícia -0,2, to je blízko 0, čo znamená, že hodnoty v súbore sú blízko normálnemu rozdeleniu v súbore. Záporné číslo znamená, že ide o plochejšie rozdelenie, teda že v súbore sú viac zastúpené skôr nižšie alebo vyššie hodnoty, než tie blízko priemeru. Naopak špicatosť (Skewness) škály deliberácia bola výrazne vyššia = 1,89, teda väčšina ľudí sa vyskytovala blízko priemeru. Šikmosť nám hovorí, či Čo sa týka šikmosti, tak v prípade deliberácie (racionality) je -1,12, teda vpravo zošikmené rozdelenie. Ľudia zaškrtali viacero vyšších hodnôt v pravej časti od priemeru. Pri intuícii je hodnota šikomosti = 0,1, teda veľmi blízka 0 a môžeme hovoriť o normálne rozložených dátach v súbore.

Reportovanie výsledkov

Vo vedeckých článkoch sa štandardne reportuje priemer spolu so smerodajnou odchýlkou. Niekedy sa uvádza minimálna aj maximálna hodnota. V našom prípade výsledky reportujeme nasledovne.

Priemerná hodnota škály deliberácie je M = 34,17; smerodajná odchýlka SD = 5,81. Minimálna hodnota Min = 9, maximálna Max = 45. Pri intuícii sme namerali nasledovné hodnoty: priemerná hodnota škály intuícia je M = 30,7; smerodajná odchýlka SD = 5,05. Minimálna hodnota Min = 13, maximálna Max = 45. Obidve škály vyplnilo 872 respondentov.

Keď sme uviedli tieto údaje potom aj iní vedci dokážu použiť tieto čísla na medzinárodné porovnávania a aj na metaanalýzy.

Reportovanie medzinárodne (V anglickom jazyku)

Príklady reportovania opisných štatistík v medzinárodnom kontexte (nesúvisia s našim príkladom):

V nasledujúcom príklade sú uvedené nielen priemery ale v zátvorkách aj variačné rozpätie a samozrejme počty respondentov podľa pohlavia.

Sixteen professional HR specialists (3 men and 13 women) with mean age 30.5 (25 – 43

years) and 16 non-experts (8 men and 8 women) with mean age 26.06 (22 – 32) participated in

the Study 2 (Čavojová, Hanák, 2014).

V druhom príklade autori uvádzajú počty respondentov ako aj priemer, variačné rozpätie a smerodajnú odchýlku.

In this experiment, 226 undergraduate Slovak students of management (148 females,

age range 18-45 years, M = 21.29, SD = 1.84) participated without incentive (Sirota, et. al. 2014).

Spracoval Róbert Hanák, November 2015

Analýza reliability

Zadanie:

Vypočítajte: a) reliabilitu pre škálu intuícia b) reliabilitu pre škálu deliberácia z dotazníka Preference for Intuition and Deliberation (PID). Použite dáta zo súboru reliabilita.

analýza reliability

Riešenie

Tento dotazník sa skladá z 9 otázok, ktoré sa viažu k deliberácii (tendenciu dôkladne uvažovať nad problémami a úlohami) a 9 otázok, ktoré sa viažu k intuícii. Tie, ktoré súvisia s deliberáciou sú označené PID_d číslo otázky, napr. PID_d1, PID_d5 atď. A podobne tie, ktoré súvisia s intuíciou sú označené napr. PID_i1, PID_i2 atď.

V ponuke Analyzovať (Analyze) si vyberieme Reliabilitu (Reliability). Následne sa nás program PSPP pýta, z ktorých položiek, v našom prípade otázok z dotazníka, chceme počítať reliabilitu. My budeme počítať reliabilitu z oboch škál zvlášť. Teda najprv si vyberieme všetky otázky, ktoré sa vzťahujú k škále deliberácia. Rovnakým spôsobom potom budeme počítať reliabilitu z otázok týkajúcich sa intuície. Vyberieme ich tak, že ich označíme v ľavej časti, kde sú všetky premenné v súbore a šípkou ich presunieme vpravo do okna označeného ako Položky (Items).

Pri analýze reliability nám program PSPP ponúka dva modely analýzy: Alpha (Cronbachova alfa) a model Split (metóda split half). Sú uvedené v prostrednej časti dialógového okna dole. Vyberieme si metódu Cronbachova alfa, ktorá je presnejšia než metóda split half.

Program nám ponúka v ľavej časti dialógového okna prostredníctvom zaškrtávacieho políčka možnosť ukázať reliabilitu skúmanej škály ak by bola konkrétna otázka zmazaná (Show descriptives for scale if item is deleted). To je veľmi dôležitá informácia, ktorá nám hovorí o tom, ako táto konkrétna položka (otázka v dotazníku) prispieva k celkovej reliabilite. Otázka môže v škále zvyšovať celkovú reliabilitu (je úzko previazaná so skúmanou latentnou premennou) alebo ju znižovať (s latentnou premennou súvisí len málo a v podstate sa pýta na niečo iné než očakávame). Preto zaškrtneme aj túto možnosť. Po zadaní všetkých týchto možností klikneme na ok, a spustíme celú analýzu.

Obr. 1 Sprievodca Analýzou Reliability

Naše výsledky

Program PSPP nám ukazuje výsledky v samostatnom súbore dole na lište, ktorý je nazvaný ako output. Najprv opíšeme výsledky pre škálu deliberácia.

V prvej tabuľke je uvedený počet prípadov (respondentov), ktorých máme 872. Sú označení ako Valid. Vylúčení (Excluded) sú takí, ktorí by nemali v súbore uvedené dáta. V našom prípade nemáme taký prípad.

V druhej tabuľke s názvom Reliability Statistics máme uvednú Cronbachovu alfu, ktorá je v našom prípade 0,82 a počet položiek.

V tretej tabuľke sú uvedené vplyvy jednotlivých položiek (otázok) na celkový výsledok ak by bola otázka vymazaná. Je tu uvedený priemer, rozptyl, upravená medzipoložková korelácia a Cronbachova alfa pre celý súbor, ak by sme nejakú konkrétnu otázku vymazali.

Napríklad, Cronbachova alfa pre celý súbor by bola 0,79 ak by bola prvá otázka PID_d1 vymazaná (Cronbach’s if item deleted). To znamená, že by sme Cronbachovu alfu znížili z pôvodných 0,82 na 0,79, teda by sme zhoršili celkovú reliabilitu škály.

Obr. 2 výsledok pre škálu PID deliberácia

Obr. 3 Výsledok analýzy pre škálu PID Intuícia

Reportovanie výsledkov:

V podstate pri každom skúmaní dotazníkov, inventárov, škál alebo testov takmer vždy reportujeme Cronbachovu alfu, ktorú sme zistili pre konkrétny dotazník. Je jedno či sme dotazník vytvorili sami a prvý krát ho na vedeckom poli prezentujeme, alebo overujeme iný, už etablovaný dotazník v našich podmienkach, či skúmame úplne niečo iné, no pri skúmaní sme použili určitý dotazník. V každom z týchto prípadov býva zvykom uviesť Cronbachovu alfu. Uvádzame nasledovné príklady:

V slovenskom prostredí:

Keďže ide o na Slovensku relatívne neznámy nástroj (nemáme informácie o jeho tuzemskom použití, aj keď je relatívne podrobne popísaný Hanákom (2013), pri každom štýle uvádzame v zátvorke aj hodnotu Cronbachovej alfy ako ukazovateľa vnútornej konzistencie subškály. Bol sledovaný racionálny (0,65), intuitívny (0,73), závislý (0,82), vyhýbavý (0,87) a spontánny (0,80) rozhodovací štýl. (Bavoľár, Orosová, 2014)

V medzinárodnom (anglickom) prostredí:

The internal consistency of PID in Slovak sample was .827 for Deliberation and .738 for

Intuition, measured by Cronbachʼ s alpha. (Ballová Mikušková, Hanák, Čavojová, 2015).

The reliability (Cronbachs a) of the scale was .87 (Saher, Lindeman, 2015).

Naše výsledky:

Naše výsledky by sme mohli reportovať nasledovne:

Vnútorná reliabilita jednotlivých škál dotazníka PID meraná Cronbachovou alfou dosahuje pre škálu deliberácia α = 0,82 a pre škálu intuícia α = 0,74.

Spracoval Róbert Hanák, 25 Novembra 2015

Exploračná faktorová analýza

Čo je faktorová analýza

Faktorová analýza na základe vzájomných vzťahov medzi viacerými premennými identifikuje tie, ktoré spolu vzájomne súvisia. Z tých, ktoré vzájomne úzko súvisia vytvára takzvané faktory, a tým redukuje počet premenných do menšieho počtu faktorov. Inými slovami, faktorová analýza pomocou skúmania vzájomných vzťahov medzi premennými (korelačnými maticami) sa snaží identifikovať faktory v skupine premenných, ktoré znížia počet premenných.

Premenné, ktoré skúmame a ktorých je zvyčajne veľa môžeme nazvať manifestnými premennými. A zredukované premenné – faktory môžeme nazvať latentnými premennými. Faktorová analýza sa prakticky používa na a) zistenie vzájomných vzťahov medzi premennými b) pri tvorbe dotazníkov c) pri redukcii veľkého počtu premenných na obmedzený počet faktorov Field (2013, str. 666.)

Predstavme si, že chceme skúmať určité premenné, na ktoré sa nevieme spýtať priamo jednou otázkou, ale len prostredníctvom viacerých iných otázok. K takýmto premenným patria napríklad introverzia, úzkosť, depresia alebo intuícia. V skutočnosti neexistuje len jedna otázka, pomocou ktorej vieme zistiť ako je človek introvertný, úzkostný, alebo ako veľmi je intuitívny. Zvyčajne musíme človeku položiť viacero otázok, niekedy celý dotazník, aby sme si spravili aký taký obraz o tom ako veľmi je, alebo nie je, intuitívny. Konštrukt Intuície je v tomto prípade latentná premenná – faktor, teda premenná, ktorú meriame pomocou viacerých iných otázok v dotazníku, ktoré v tomto prípade nazývame manifestné premenné.

Pri skúmaní konštruktu intuície môžeme použiť dotazník, ktorý vytvorila nemecká výskumníčka Cornelia Betschová (2004). V dotazníku sa snaží identifikovať intuíciu pomocou aj týchto otázok: „Pozorne načúvam svojim najhlbším pocitom“, alebo „Moje pocity hrajú dôležitú úlohu v mojich rozhodnutiach.“ Podobných otázok vytvorila 9, a predpokladala, že tieto otázky dokážu zachytiť konštrukt intuície. Každá otázka sa pýta na intuíciu a jej prejavy trochu iným spôsobom, ale všetky súvisia s intuíciou. Súčasne dotazník obsahuje aj otázky, ktoré majú merať konštrukt uvažovania, deliberácie a tiež pomocou 9tich otázok (manifestných premených). V tomto príklade budeme pracovať s týmto dotazníkom.

Predtým, než sa pustíme do samotnej analýzy tak si ešte vysvetlíme niekoľko dôležitých pojmov. Začneme s tým, že existujú dva typy faktorovej analýzy: exploračná a konfirmačná. Exploračná faktorová analýza bola navrhnutá za účelom objavovať (explore) skryté faktory v rámci skupiny premenných, kedy vopred presne nevieme aké vzťahy máme medzi nimi očakávať. Naopak konfirmačná faktorová analýza bola vytvorená za účelom potvrdiť, overiť už vopred známu, očakávanú existenciu faktorov. Preto pre nové dotazníky, skupiny premenných používame exploračnú faktorovú analýzu, a pre už existujúce, overené a známe používame konfirmačnú faktorovú analýzu. Softvér PSPP umožňuje však počítať len exploračnú faktorovú analýzu. Pri počítaní exploračnej faktorovej analýzy je počet respondentov dôležitý. Field (2013) uvádza, že na každú otázku z dotazníka potrebujeme minimálne 10 až 15 respondentov. Čiže ak má náš dotazník 10 otázok, potom potrebujeme minimálne 100 až 150 respondentov.

K ďalším dôležitým pojmom patrí faktorové zaťaženie, sýtenie alebo faktorový náboj (factor loading), ktorý znamená aká časť variability konkrétnej premennej X_i je vysvetlená konkrétnym faktorom F. Halama (2011) ju opisuje aj ako koreláciu s faktorom, ktorá rovnako ako korelačný koeficient nadobúda hodnoty od -1 po 0 v prípade nepriameho vzťahu alebo od 0 po 1 v prípade priameho vzťahu. Čím sú hodnoty bližšie 1, tým viac premenná sýti daný faktor. Výsledkom exploračnej faktorovej analýzy v programe PSPP je aj faktorová matica, ktorá obsahuje faktorové zaťaženie všetkých premenných (otázok z dotazníka) k jednotlivým faktorom. V matici uvidíme aký vzťah má každá otázka k jednotlivému faktoru, či ho sýti pozitívne, negatívne a ako silno.

Vlastná hodnota (eigenvalue) je podľa Hendla (2009, str. 508) : „číslo, ktoré vo faktorovej analýze udáva pre daný faktor, koľko vysvetľuje variability zo systému premenných, ktoré sledujeme.“ Čím vyššia hodnota, tým faktor viac vysvetľuje z variability premenných. Vlastná hodnota je zvyčajne malé číslo od 0 po približne 10, niekedy i viac (závisí od dát) a nás zaujímajú hodnoty vyššie než 1.

Ak by sme skúmané premenné zobrazili graficky ako body v priestore okolo centrálneho bodu a chceli by sme ich priraďovať k jednotlivým faktorom, tak by sme do priestoru nakreslili dve úsečky, ktoré sa pretínajú v strede. Úsečky by boli vlastne faktory a podľa toho aký typ rotácie úsečiek – faktorov by sme zvolili tak by boli alebo neboli na seba kolmé. Ak by sme ich rotovali avšak vždy by boli na seba kolmé, tak tento typ rotácie sa nazýva ortogonálny. Tu predpokladáme, že sú faktory na sebe nezávislé, vzájomne nekorelujú a sú jedinečné. Alebo by mohli zvierať akýkoľvek iný uhol a boli by teda vzájomne na seba šikmé. Rotácia faktorov sa používa aj v programe PSPP, ktorý nám ponúka štyri typy rotácie:

Žiadnu (None)
Varimax je kolmý (ortogonálny) typ rotácie. V tomto prípade program rotuje osi, avšak vždy sú jednotlivé osi na seba kolmé. Súčasne každá premenná sýti len jeden faktor, teda minimalizuje počet premenných, ktoré majú vysoký náboj. Tento typ rotácie je v programe prednastavený, pretože sa najľahšie interpretuje a má aj najširšie možnosti aplikácie.
Quartimax minimalizuje počet faktorov a je taktiež kolmý typ rotácie.
Equimax je kombináciou hore uvedených. Snaží sa vybrať minimálny počet faktorov a súčasne každá premenná sýti len jeden faktor. Je to tiež ortogonálny typ rotácie.

Sutinový graf (scree plot) je graf zložený z vlastných hodnôt (eigenvalues), ktoré sú na Y-novej osi a faktorov na X-ovej osi zoradených od najvyšších po najnižšie. Graf vždy klesá, a pri interpretácii je dôležitý jeho tvar. Prudký pokles krivky grafu je ideálny, nakoľko znamená, že máme málo faktorov s vysokými vlastnými hodnotami (eigenvalues). Teda manifestné premenné (otázky z dotazníka) dobre sýtia jednotlivé faktory, ktorých nie je veľa.

Podrobnejšie a v súvislostiach si tieto pojmy vysvetlíme na riešení a interpretácii nasledovného príkladu.

Zadanie úlohy:

Pomocou exploračnej faktorovej analýzy preskúmajte nemecký dotazník dotazník PID ( Preference for Intuition and Deliberation, Betsch, 2004) na vzorke slovenskej populácie. Príklad č. 1 – Faktorová analýza. Dotazník má 18 otázok a polovica z nich by mala sýtiť latentnú premennú intuíciu a druhá polovica otázok ( inými slovami aj manifestných premenných) latentnú premennú nazvanú deliberácia, teda sklon k uvažovaniu a racionalite. V našom príklade vidíme, že každá z otázok je označená na základe nasledovného princípu: PID_1d, kde 1d znamená, že ide o prvú otázku zo subškály deliberácia. Teda tie, ktoré súvisia s deliberáciou sú označené PID_d číslo otázky, napr. PID_d1, PID_d5 atď. A podobne tie, ktoré súvisia s intuíciou sú označené napr. PID_i1, PID_i2 atď. U výsledkov predpokladáme, že nájdeme dva dominantné faktory, ktoré budú nezávislé a otázky zo subškály deliberácia budú sýtiť 1 faktor a otázky zo subškály intuícia, uvažovanie budú sýtiť druhý faktor.

Pred samotnou faktorovou analýzou ešte poznamenávam nasledovné. Ak by sme skúmali už existujúci a v našej populácii overený dotazník mali by sme použiť konfirmačnú faktorovú analýzu. My však skúmame dotazník na Slovensku zatiaľ neuvedený, ktorého pôvodná vzorka bola zložená z nemeckých občanov. Preto môžeme argumentovať, že objavujeme (exlore) aké faktory dotazník bude mať pre slovenskú populáciu.

Riešenie:

Otvoríme si súbor s názvom Príklad č. 1 – Faktorová analýza. V ponuke Analyzovať (Analyze) si vyberieme Exploračnú faktorovú analýzu (Factor Analysis…). Najprv presunieme všetky otázky z dotazníka pre intuíciu označené PID_i1 až i9 ako aj pre deliberáciu označené PID_d1 až PID_d9, teda spolu 18 premenných, vpravo do poľa Premenné (Variables). Ďalej, po otvorení dialógového okna nám program v spodnej časti menu ponúka dve možnosti: Extrakciu (Extraction) a Rotácie (Rotation). Musíme vyplniť obidve a tak si klikneme najprv na Extrakciu a budeme postupovať nasledovne. Pri našej analýze vyberieme metódu: Analýzu hlavných komponentov (Principal component analysis), ďalej zaškrtneme Korelačnú maticu (Corelation matrix) a Sutinový graf (Scree plot). A dáme vyextrahovať vlastné hodnoty väčšie ako 1. Počet faktorov nebudeme limitovať. Maximálny počet iterácií nenastavujeme. V prípade, že softvér nebude chcieť spustiť analýzu, potom môžeme pridať znamienkom + o 1 iteráciu viac, čo zvyčajne už analýzu spustí. Na záver klikneme na Pokračovať(Continue).

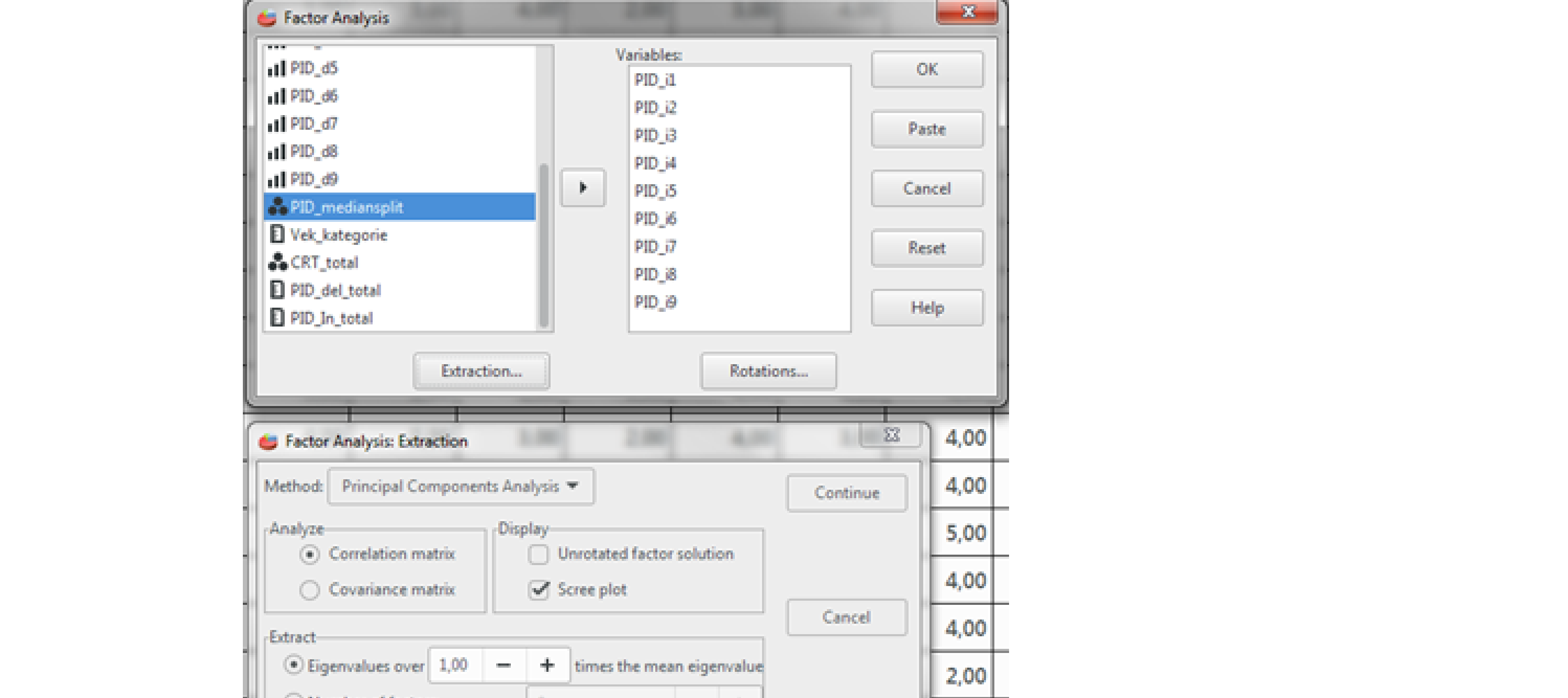
Obr. 1 Dialógové okno Extrakcia a Rotácia faktorov

Potom klikneme na dialógové okno Rotácie (Rotations) nám ponúka tri metódy rotácie. Vyberieme Varimax metóda (kolmý typ rotácie), ktorá je v programe. Následne klikneme Pokračovať (Continue) a spustíme celú analýzu kliknutím Ok.

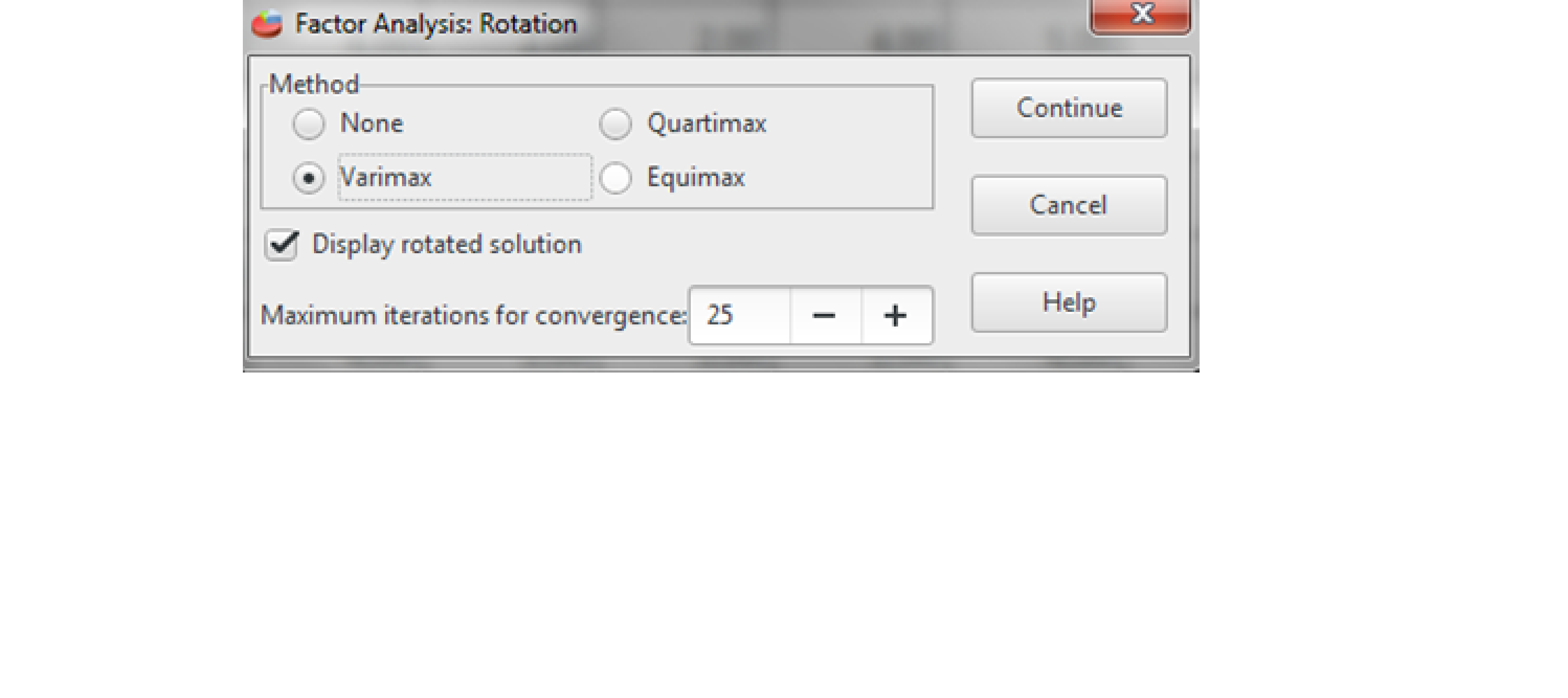
Obr. 2 Dialógové okno rotácie faktorov

Výsledky:

Výsledkom faktorovej analýzy je viacero tabuliek a Sutinový graf (Scree plot), ktoré si opíšeme podrobnejšie. Začneme grafickou interpretáciou sutinového grafu. V Sutinovom grafe (Scree plot) vidíme (obr. 1), že existujú minimálne dva dominantné faktory, ktorých vlastná hodnota (eigenvalue) je vyššia než 1. Podľa predpokladov dotazník má merať 2 faktory: intuíciu a uvažovanie, čiže prvotné grafické výsledky zbežne potvrdzujú naše predpoklady. No na robenie štatistických úsudkov potrebujeme pracovať s exaktnými číslami, ktoré sú uvedené v tabuľkách na obrázku dole.

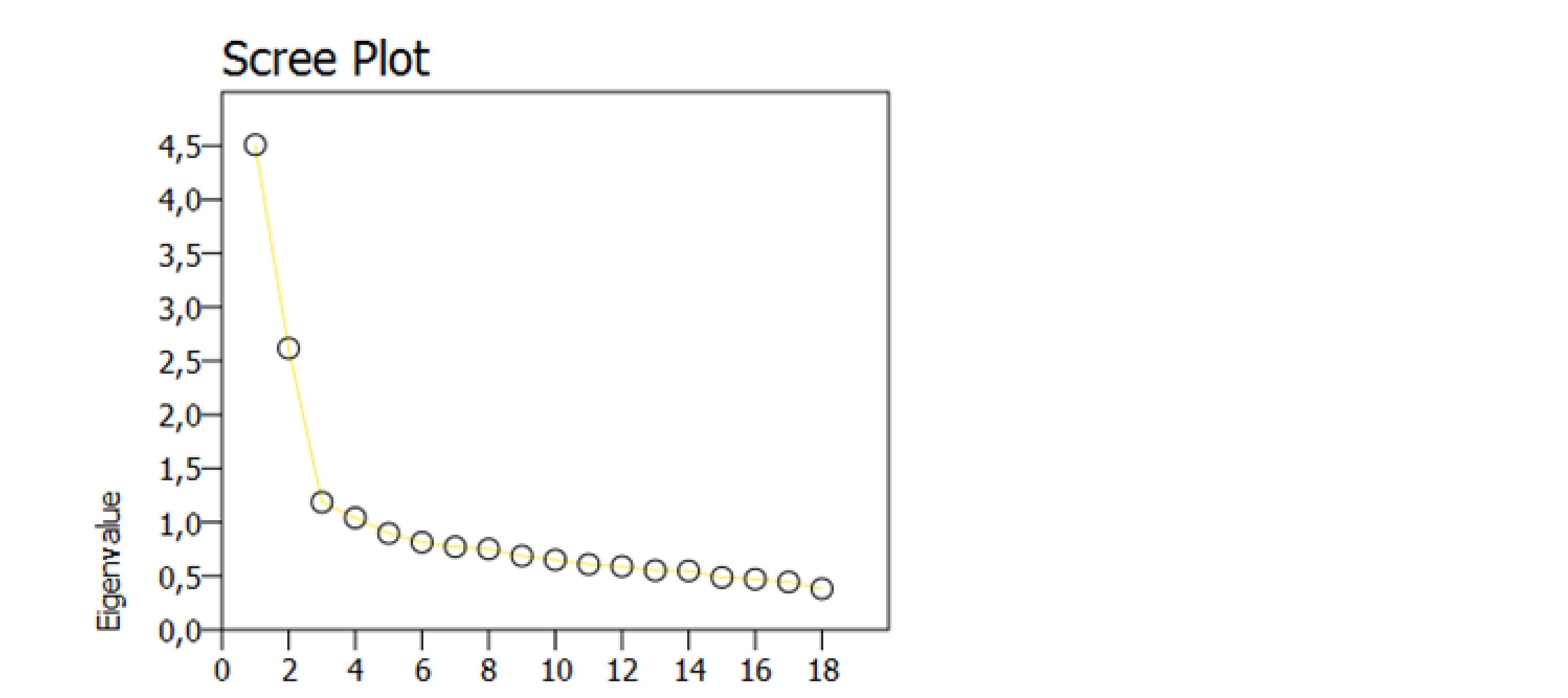
Obr. 3 Sutinový graf (Scree plot)

V nasledovnej tabuľke podrobnejšie opíšeme grafické zobrazenie faktorov v sutinovom grafe. V prvom stĺpci sú uvedené všetky faktory. V druhom je Vlastná hodnota jednotlivých faktorov (Eigenvalues) v stĺpci Total. V druhom stĺpci je uvedené percento variability, ktorú vysvetľuje konkrétny faktor. A v poslednom stĺpci je uvedené kumulatívne percento. Zaujímajú nás faktory, u ktorých je Vlastná hodnota (Eigenvalues) vyššia než 1 v našej tabuľke vidíme, že 4 faktory majú vlastnú hodnotu vyššiu než 1. Prvý, najvýznamnejší faktor vysvetľuje 25,05 % variability, druhý 14,54% a spolu 39,59%. To nie je zvlášť veľa nakoľko dotazník mal merať len 2 faktory a my sme zistili ďalšie dva s vlastnou hodnotou väčšou ako 1 a tiež Celkové percento variability (Cumulative %) vysvetlené týmito faktormi je pomerne nízke.

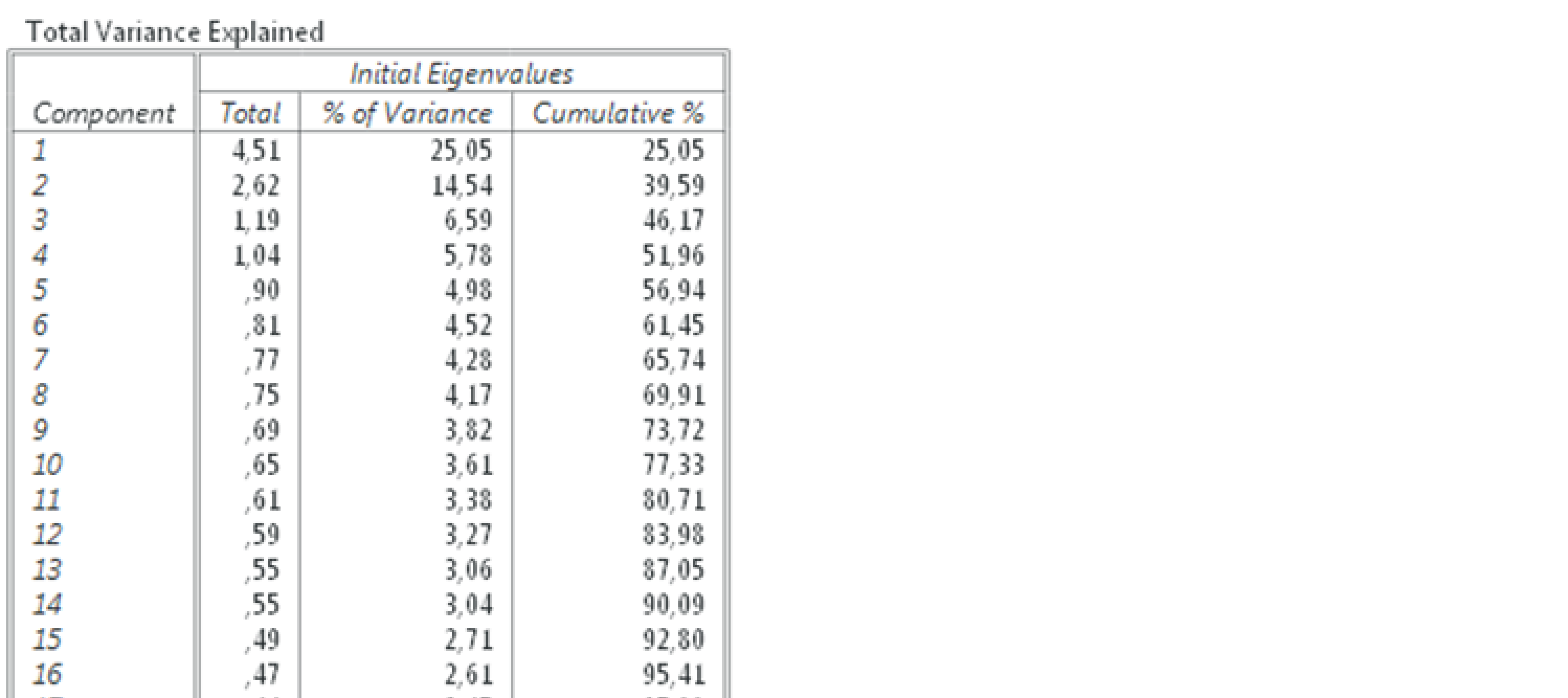
Obr. 3 Identifikované faktory, vlastné hodnoty (eigenvalues) a percentá vysvetlenej variability

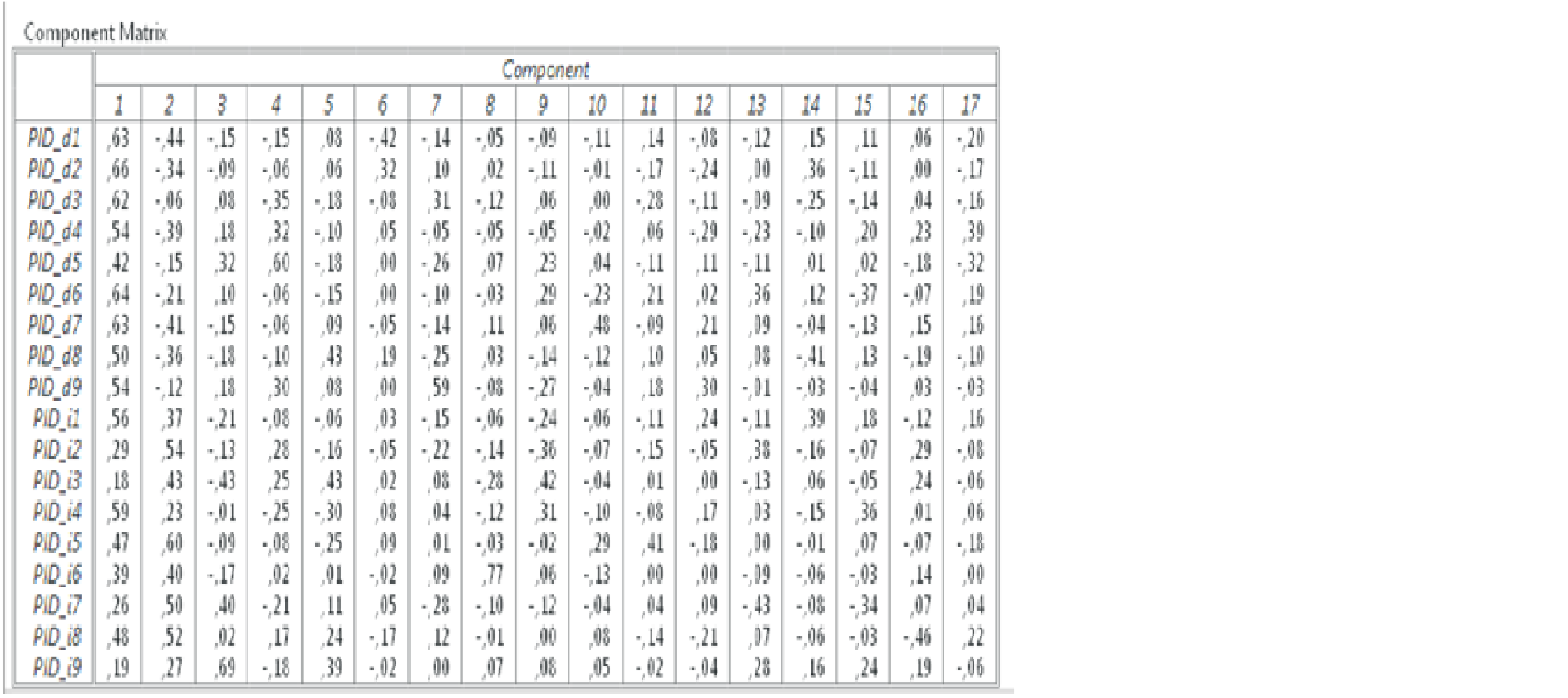
Obr. 4 Faktorová matica pre všetky faktory a všetky otázky z dotazníka PID

Na obrázku č. 4 je uvedený faktorový náboj, sýtenie pre každú otázku z dotazníka. V prvom riadku je otázka PID_d1, čiže zo škály deliberácia, uvažovanie. Táto otázka má pre prvý najsilnejší faktor sýtenie 0,63 a pre druhý faktor záporné sýtenie rovné -0,44. Rovnako ostatné otázky zo škály uvažovanie majú pre prvý faktor pozitívne sýtenie. Čiže všetky otázky zo škály deliberácia pozitívne korelujú s faktorom č. 1, a zároveň negatívne korelujú s faktorom č. 2. Preto prvý najsilnejší faktor (č. 1) môžeme nazvať uvažovanie – deliberácia.

Veľmi problematické sú otázky zo subškály intuícia PIDi_1 až PIDi_9, ktoré pozitívne sýtia aj prvý faktor (č. 1) aj druhý faktor (č.2). Jednotlivé otázky zo škály intuícia už z etablovaného dotazníka PID majú mať pozitívny vzťah k intuícii a negatívny k deliberácii. A nie pozitívny k obidvom. Napr. otázka PIDi_1 koreluje pozitívne s faktorom deliberácia 0,56 (mala by korelovať negatívne) a tiež pozitívne 0,37 s druhým faktorom (intuícia). Podľa očakávaní a predpokladov by mali byť všetky otázky z intuície rozhodne v negatívnom vzťahu k prvému faktoru (deliberácia), teda mali by byť záporné a v pozitívnom k druhému faktoru (intuícia). Pretože takto tieto otázky merajú aj deliberáciu a nie len intuíciu, ako by mali.

Interpretácia:

Dotazník PID bol konštruovaný ako dvojfaktorový dotazník, ktorý mal merať Intuíciu a Deliberáciu, Uvažovanie (Racionalitu). Preto sa očakáva, že každá otázka súvisiaca s Intuíciou bude vysoko sýtiť faktor intuícia a každá otázka súvisiaca s deliberáciou zas faktor deliberácia. Zároveň sa však očakáva aj že každá otázka v pozitívnom vzťahu s faktorom č. 1 – deliberácia bude v negatívnom vzťahu k faktoru č. 2 – intuícia. To sa potvrdilo. Problémom však je že otázky z intuície, ktoré by mali sýtiť pozitívne len faktor č. 2 (intuíciu) pozitívne sýtia aj faktor č. 1(deliberáciu). Teda otázky z intuície „merajú“ aj uvažovanie, deliberáciu. To je veľmi problematické pretože otázka, ktorá má merať intuíciu nemôže súčasne merať aj uvažovanie (deliberáciu). Na základe výsledkov konštatujeme, že otázky zo škály intuícia z dotazníka PID sýtia pozitívne obidva faktory a nie sú jednoznačne priradené len k intuícii ale aj k deliberácii.

Uvádzanie výsledkov:

Na analýzu vnútornej štruktúry dotazníka PID (Betsch, 2004) slovenskom prostredí bola zvolená exploračná faktorová analýza, pomocou metódy hlavných komponentov (principal axis factoring), ortogonálna rotácia Varimax. V skúmanej vzroke sme identifikovali 4 faktory, ktorých vlastná hodnota (Eigenvalue) bola vyššia ako 1. Prvý faktor vysvetľoval 25,05 % variability a druhý 14,54 %, spolu vysvetľovali spolu 39,59 %, tretí faktor 6,59% a štvrtý 5,78%.

Všetky otázky zo subškály Deliberácia, ktoré mali sýtiť latentný faktor Deliberáciu boli v pozitívnom vzťahu s týmto faktorom a faktorové zaťaženie sa pohybovalo od 0,42 pre PID_d5 po 0,66 pre PID_d2. Pri latentnej premennej Intuícia bolo faktorové zaťaženie všetkých otázok merajúcich intuíciu bolo v pozitívnom vzťahu a pohybovalo sa od 0,19 pre PID_i9 po 054 pre PID_i9. Avšak súčasne všetky otázky zo subškály Intuícia taktiež pozitívne sýtili faktor deliberácia, čo je priamom rozpore s predpokladmi.

Spracoval Róbert Hanák, 10. Novembra 2015

Program nereaguje. Softvér som nainštaloval, ale keď klikám na panely s ponukou nereaguje.

Softvér PSPP je vyvíjaný skupinou nadšencov, ktorí majú obmedzený čas i zdroje, a preto softvér nie je tak rozsiahlo, dôkladne a prísne testovaný na rôzne zlyhania alebo nekompatibilitu ako softvéry veľkých súkromných výrobcov. Znova skontrolujte, či ste vybrali správny softvér pre váš operačný systém (32 verzus 64 bitový u Windowsov). Ak stav pretrváva, odporúčam preinštalovať. V prípade, že sa ani potom nič nezmenilo, skúste nainštalovať staršiu verziu.