Wilcoxonov test

Wilcoxonov test patrí do skupiny neparametrických testov, ktoré používame ak naše dáta nemajú normálne rozloženie. Používame ho na porovnanie rovnakej skupiny respondentov v dvoch podmienkach. Napríklad otestujeme respondentov pred experimentálnou manipuláciou a po nej a skúmame či experiment spôsobil štatisticky významne rozdielne skóre.  Zjednodušene by sme mohli povedať že je ekvivalentom párového t testu.

Zadanie:

Študenti boli požiadaní aby posúdili kvalitu podnikateľského zámeru opísanú v podnikateľskom pláne a pridelili mu body (skóre) od 0 – určite skrachuje po 10 – určite bude úspešný. Plán posudzovali v dvoch podmienkach: I, v podmienke časového stresu (mali prideliť body do 3 minút od otvorenia súboru)  a v II, bez časového obmedzenia. Zaujíma nás, či sa v prvom a v druhom hodnotení celkové skóre pre podnikateľský plán zmenilo. Konkrétnejšie predpokladáme, že v podmienke bez časového stresu budú hodnotiť podnikateľský plán negatívnejšie a pridelia mu menej bodov ako v časovom strese.

H₁: Študenti v podmienke časového stresu ohodnotili podnikateľský plán pozitívnejšie ako v podmienke bez časového stresu.

H₀: Celkové hodnotenie podnikateľského plánu sa medzi podmienkami štatisticky významne nelíši.

Riešenie:

Najprv si overíme či sú naše dáta rozložené normálne. V prípade ak sú rozložené normálne, potom použijeme Párový t test a ak nie sú tak použijeme Wilcoxonov test. Výsledky Kolmogorovho – Smirnovho testu nám ukazujú, že naše dáta nie sú rozložené normálne ani pri prvej(v časovom strese) a ani pri druhej podmienke (bez časového stresu).

Obr. 1 Výsledok Kolmogorovho – Smirnovho testu.

Keďže naše dáta nie sú rozložené normálne na porovnanie prvého a druhého hodnotenia použijeme Wilcoxonov test. Budeme postupovať nasledovne. Klikneme na Analyzovať (Analyze) a vyberieme si Neparametrické Štatistiky (Non-parametric statistics) a ďalej Testy pre dve súvisiace skupiny (Two – Related – Samples Tests). Následne presunieme premenné Celk_skor_I a Celkove_skr_II do okna Testované Páry (Test Pair(s)) a v spodnej časti okna zaškrtneme Wilcoxonov test (Wilcoxon). Potom klikneme Ok.

Obr. 2 Sprievdca Wilcoxonovým testom

Výsledky:

Výsledkom sú dve tabuľky. V prvej sú uvedené vzájomné vzťahy medzi jednolivými hodnoteniami. Máme 20 prípadov kedy bolo prvé hodnotenie podnikateľského plánu nižšie než druhé (Celkové_skr_II) a 33 kedy bolo prvé hodnotenie vyššie než druhé. 20 hodnotení bolo rovnakých.

Výsledky samotného Wilcoxonovho testu sú uvedené v druhej tabuľke kde Z = -2,09 na hladine významnosti p = 0,037, teda sú štatisticky významné.  Na základe týchto výsledkov prijímame alternatívnu hypotézu  H₁.

Obr. 3 Výsledok Wilcoxonovho testu

Veľkosť účinku vypočítame pre Wilcoxonov test nasledovne:

Uvádzanie výsledkov:

Respondenti ohodnotili rovnaký podnikateľský plán v podmienke časového stresu pozitívnejšie ako bez časového obmedzenia a výsledky boli štatisticky významné Z = -2,09, p = 0,037 s malým efektom účinku r = – 0,24.

Spracoval Róbert Hanák, Február 2016

Analýza rozptylu (ANOVA – Analysis of Variance)

Je parametrická štatistická metóda vytvorená na vzájomné porovnávanie skupín, ktorých počet je viac než dve. Zjednodušene by sme mohli povedať, že je to t test pre viac ako dve skupiny. Existuje viacero typov analýzy rozptylu  ( viacero ANOV), no my sa v tejto časti zameriame na základnú a najjednoduchšiu z nich – ANOVU pre 1 faktor (One way ANOVA). Pri tejto ANOVE porovnávame viacero skupín (viac než 2) a hľadáme či sa štatisticky významne odlišujú len v 1 faktore.

Zadanie:

V príklade č. 7. Canvas metódy a startup je opísaný podnikateľský zámer pomocou metódy Canvas. Podnikatelia, žiadajúci o financie od nezávislých investorov, opísali svoj zámer a ten bol následne obodovaný metodikou Canvas. Podľa toho ako dobre, podrobne a odborne opísali svoj zámer, dostávali body za jednotlivé kategórie ako napríklad segmenty zákazníkov, ponúkaná hodnota a ostatné, ktoré sa sčítali a vzniklo Celkové skóre Canvas, ktoré je v našom príklade č. 7 posledný stĺpec s názvom: Canvas_total_score. Čím je toto skóre vyššie, tým podrobnejší, odbornejší a kvalitnejší podnikateľský plán predložili. Rôzni podnikatelia mali za sebou rôzne skúsenosti a pre väčšinu z nich bol tento ich zámer vôbec prvým pokusom začať podnikať. Iní už vlastnili existujúcu firmu a niektorí mali aj dve, či dokonca tri firmy. V stĺpci s názvom: N je uvedený počet firiem, ktoré podnikatelia založili v minulosti. Na základe počtu založených firiem rozdelíme podnikateľov do 4 skupín (0 – nemá firmu, 1 – založil jednu firmu, 2 – dve firmy, 3 – tri firmy). Zaujíma nás, či tí, ktorí majú skúsenosti v podnikaní (založili 1 alebo viac firiem), dokážu lepšie vypracovať podnikateľské zámery a plány. Predpokladáme, že  premenná:  Celkové Canvas skóre sa bude medzi skupinami líšiť. Na základe týchto predpokladov sme si stanovili nasledovné hypotézy:

H₁: Podnikatelia rozdelení do štyroch skupín podľa počtu založených firiem sa štatisticky významne líšia v Celkovom Canvas skóre.

H₀ : Neexistuje štatisticky významný rozdiel v Celkovom Canvas skóre medzi podnikateľmi, ktorí založili rôzny počet firiem.

Riešenie:

Postup riešenia je nasledovný:

1. Krok: Overiť normalitu rozloženia dát u skúmanej premennej (Celkové Canvas skóre).
2. Krok: Ak sú dáta rozložené normálne použijeme parametrickú metódu na porovnanie skupín, v našom prípade Analýzu rozptylu – ANOVU, ak nie sú potom použijeme neparametrickú metódu pre viac skupín než dve, a tou je Kruskal – Walisov Test.

Prvým krokom je teda overiť normalitu rozloženia dát. Použijeme na to Kolmogorov – Smirnov test. Postup pri tomto teste opisujeme napríklad v záložke na stránke s názvom: Meranie vzájomných vzťahov u ordinálnych premenných. A preto tu uvádzame už iba výsledok. Z výsledku vidíme, že hodnota Sigma je 0,476, čo je oveľa viac než hladina významnosti 0,05, čo znamená, že dáta sú rozložené normálne.

Obr.1 Výsledok Kolmogorovho – Smirnovho testu.

Krok 2. Nakoľko z výsledkov Kolmogorovho – Smirnovho testu usudzujeme, že dáta sú rozložené normálne, potom môžeme aplikovať parametrický test na porovnanie skupín ANOVA. Postup je nasledovný.

Klikneme na Analyzovať (Analyze) a potom na  Porovnať priemery (Compare Means) a vyberieme Jednofaktorovú Analýzu rozptylu (One – Way ANOVA). V sprievodcovi presunieme premennú Canvas_total_score do okna Závislé premenné  (Dependent variable(s)). Ďalej vyberieme premennú Počet založených firiem v minulosti – N a presunieme ju do políčka Faktor (Factor). V zaškrtávacích políčkach dole zaškrtneme Opisné štatistiky (Descriptives) a test Homogenity dát (Homogeneity). Na záver klikneme Ok.

Obr. 2 Sprievodca Analýzou rozptylu (ANOVA)

 Výsledky:

Program PSPP ako výsledok vytvorí tri tabuľky. V prvej tabuľke sa nachádzajú opisné štatistiky pre každú skupinu. Máme 4 skupiny žiadateľov čo sa týka ich predchádzajúcich skúseností v podnikaní. Prvá skupina je najpočetnejšia (n = 136), označili sme ju 0,  a táto nezaložila v minulosti žiaden podnik. Ich priemerné skóre v bodovaní Canvas je: M = 32,13 bodu, smerodajná odchýlka SD = 14,63 a v riadku sú uvedené aj ďalšie opisné štatistiky pre skupinu 0. V druhom riadku sú uvedené opisné štatistiky pre Celkové Canvas skóre u skupiny podnikateľov, ktorí založili 1 firmu a treťom i štvrtom riadku je princíp rovnaký ako v prvých dvoch.  Keď porovnáme priemery (stĺpec Mean v prvej tabuľke) vidíme, že skupiny sa medzi sebou pomerne výrazne líšia v priemerných hodnotách z Celkového Canvas skóre, otázkou však je, či tieto rozdiely sú aj štatisticky významné. Na to nám odpovie tretia tabuľka.

V druhej tabuľke sú výsledky testu pre normalitu rozloženia dát, v tomto prípade výsledky Levenovho testu = 0,3 pri hladine významnosti p = 0,992. Táto úroveň hladiny významnosti je vysoko nad podmienkou p < 0,05, a teda test je nevýznamný, čo znamená, že dáta pre premennú  Celkové skóre canvas sú rozložené normálne. Tieto výsledky sú doplnením Kolmogorovho – Smirnovho testu a sú s ním v zhode. Z praktického hľadiska stačí použiť jeden z nich.

Tretia tabuľka obsahuje výsledky samotnej ANOVY a je pre nás najdôležitejšia. Hovorí nám o tom, či sa naše 4 skupiny medzi sebou štatisticky významne líšia. V poslednom stĺpci Sig. je uvedená hladina významnosti, ktorá je menej než 0,001, čo znamená, že skupiny sa medzi sebou štatisticky významne líšia čo sa týka premenej: Celkové skóre Canvas. Na základe týchto výsledkov prijímame prvú hypotézu H₁  a zamietame nulovú hypotézu.

Obr. 3 Výsledok analýzy rozptylu (ANOVA)

Veľkosť účinku (effect size)

Vypočítame ju z nasledovného vzorca, kde dáta použijeme z poslednej tabuľky výsledkov, kde rozptyl medzi skupinami (Between Groups) sa označuje aj ako SS_M = 4783,82 a celkový rozptyl (Total) SS_T = 46 607,87. Dosadením do vzorca  a vypočítaním dostaneme hodnotu r  = 0,32, čo je stredná hodnota účinku ( je väčšia ako 0,3).

Uvádzanie výsledkov:

Jednotlivé skupiny podnikateľov, vytvorené podľa počtu založených firiem v minulosti, sa vzájomne štatisticky významne líšia v tom, aké Celkové skóre Canvas dosiahol nimi predložený podnikateľský plán, F(3,196)= 7,47, p < 0.001, so stredným efektom účinku r = 0,32.

Spracoval Róbert Hanák, November 2016

Párový t – test sa používa na porovnávanie hodnôt premennej u rovnakého respondenta v dvoch rôznych experimentálnych podmienkach. Napríklad pred školením a po školení.

Zadanie:

Študenti boli požiadaní aby posúdili kvalitu podnikateľského zámeru opísanú v podnikateľskom pláne a pridelili mu body od 0 – určite skrachuje po 10 – určite bude úspešný. Podnikateľský plán bol opísaný 25 podnikateľskými charakteristikami ako: cena produktu, súčasná konkurencia, vzhľad  atď. Študenti však okrem nadpisu napr. cena, obsah vlastností hneď nevideli, ale mohli si na ne kliknúť a potom sa im objavil obsah. Teda aká je napríklad cena u daného produktu.

Zaujíma nás koľko podnikateľských charakteristík z 25 dostupných si študenti skutočne otvorili predtým než pridelili finálne skóre celému podnikateľskému zámeru. Každý študent sa rozhodoval v dvoch podmienkach: A) v časovom strese, kde do 3 minút musel prideliť finálne skóre a potom B) kde posudzoval rovnaký podnikateľský plán, ale už nemal žiadne časové obmedzenie. Predpokladáme, že študent si v časovom strese otvoril menej podnikateľských charakteristík ako bez časového obmedzenia. Na základe tohto predpokladu sme si stanovili hypotézy nasledovne:

H₁: Študenti si v podmienke časového stresu otvorili štatisticky významne menej podnikateľských charakteristík pri posudzovaní podnikateľského plánu ako v podmienke bez časového obmedzenia.

H₀: Rozdiel medzi počtom otvorených podnikateľských charakteristík pri posudzovaní podnikateľského plánu v podmienke časového stresu sa nelíši od podmienky bez časového obmedzenia.

Porovnajte počet otvorených podnikateľských charakteristík v časovom strese a bez časového stresu.

Riešenie:

Nakoľko máme len jednu skupinu respondentov a každý z nich vypĺňal úlohu dva krát, teda máme 1 a 2 hodnotenie od tej istej osoby, tak použijeme párový t – test. Budeme pracovať s príkladom č. 2. Študenti body a pamäť.  Postup riešenia je nasledovný:

Klikneme na Analyzovať (Analyze) a potom na  Porovnať priemery (Compare Means) a vyberieme Párový t test (Paired Sample t – test).  Vyberieme premenné počet otvorených podnikateľských charakteristík v časovom strese (Pocet_otv_I) a počet otvorených podnikateľských charakteristík bez časového stresu (Pocet_otv_I). Ďalej klikneme na Možnosti (Options) a tu ponecháme nastavený interval spoľahlivosti  (Confidence Interval) na úrovni 95 %. Potom klikneme Pokračovať (Continue) a Ok.

Obr.1  Sprievodca párovým t -testom (Paired Samples T – test)

Výsledok a interpretácia:

Výsledkom analýzy sú tri tabuľky. V prvej tabuľke sú opisné štatistiky. Počet otvorených podnikateľských charakteristík v časovom strese  (n = 74– počet študentov) bol v priemer M = 12,04, SD = 4,94 a počet otvorených podnikateľských charakteristík bez časového stresu  (n = 74 – počet  je rovnaký pretože porovnávame tú istú skupinu) bol priemer M = 10,00 a smerodajná odchýlka SD = 3,97. Ako vidíme počet otvorených podnikateľských charakteristík v časovom strese bol dokonca väčší než bez časového obmedzenia. To je úplne mimo predpokladov aké sme si stanovili, keďže sme očakávali, že práve časový stres povedie k tomu, že si budú otvárať menej podnikateľských charakteristík.

V druhej tabuľke je uvedený korelačný koeficient medzi premennými, ktorý je v našom prípade r = 0,35, p = 0,002.

V tretej tabuľke sú uvedené výsledky samotného testu, kde t (73)  = 3,42, p = 0,001. Rozdiel medzi prvým a druhým hodnotením je štatisticky významný, pretože hodnota p je nižšia než 0,05. V prvom stĺpci s názvom Priemer (Mean) je uvedený rozdiel medzi priemernými hodnotami v prvej a v druhej podmienke, v našom prípade 12,04 -10,00 = 2,04. V hypotéze 1 sme vyslovili tvrdenie, že skupiny sa budú medzi sebou štatisticky významne líšiť, avšak stanovili sme predpoklad, že v podmienke časového stresu si otvoria kritérií menej. No výsledky vyšli naopak (otvorili si viacej), preto nemôžeme hypotézu H₁ prijať a prijímame nulovú hypotézu.

 Obr. Výsledok párového t -testu.

Na to aký veľký rozdiel medzi skupinami je musíme ešte vedieť posledný koeficient, ktorý sa nazýva veľkosť účinku(efect size).  Program PSPP neuvádza veľkosť účinku pre párový test, avšak v odbornej literatúre sa vyžaduje, a preto ho musíme dopočítať ručne. Vzorec je rovnaký ako pri dvojvýberovom t test s rovnosťou rozptylov (independent sample t – test). V našom prípade je postup nasledovný:

Veľkosť účinku výpočet (efect size):

Uvádzanie výsledkov:

Respondenti (n = 74) v časovom strese si otvorili viac podnikateľských charakteristík (M = 12,04, SD = 4,94) pri posudzovaní podnikateľského plánu ako v prípade, keď neboli časovo limitovaní (M = 10,00, SD = 3,97). Rozdiel bol štatisticky významný t (73)  = 3,42, p = 0,001 so strednou veľkosťou účinku r = 0,37.

Spracoval Róbert Hanák, 3 Marec 2016

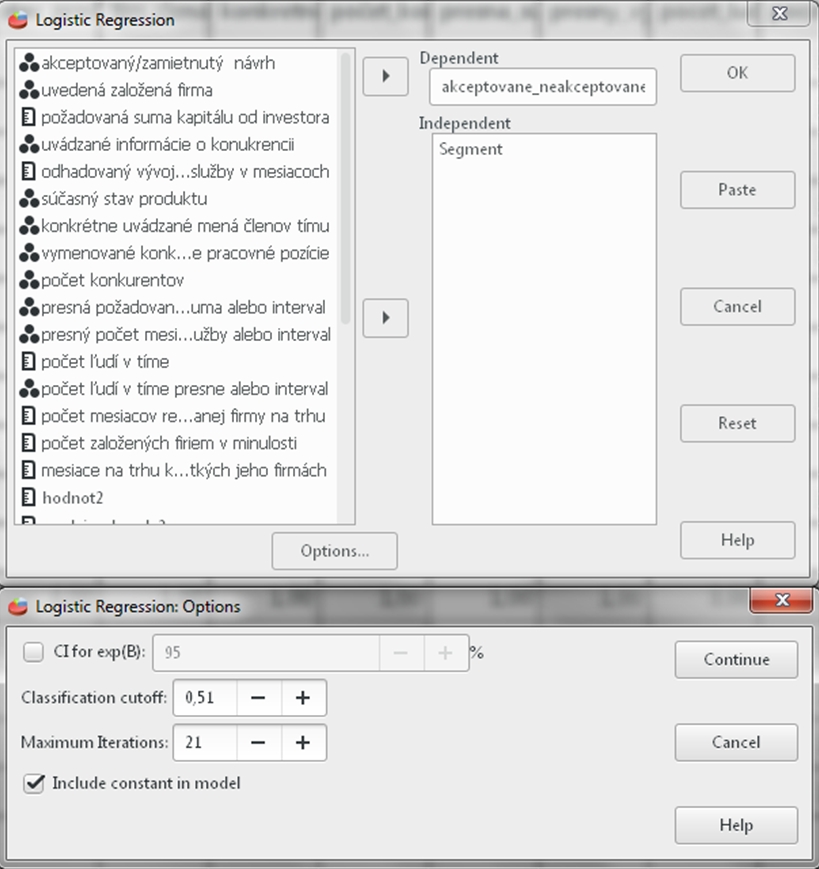
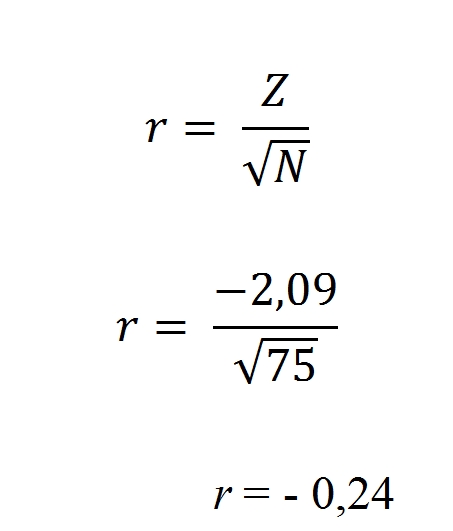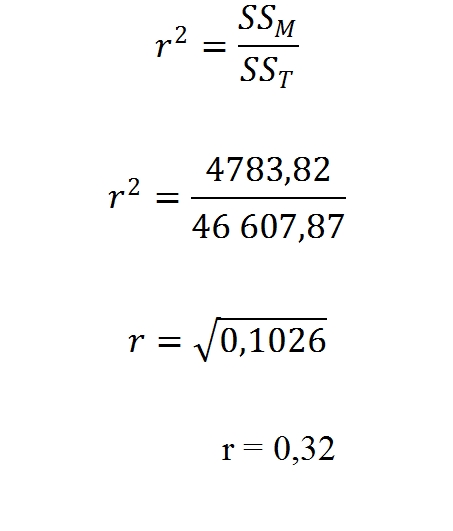Analýza závislostí u ordinálnych premenných

Ordinálne premenné sú poradové premenné a v mnohých prípadoch ide o výroky v dotazníku ako napríklad: veľmi súhlasím, súhlasím, čiastočne súhlasím, čiastočne nesúhlasím, nesúhlasím a veľmi nesúhlasím. Program PSPP ponúka viacero štatistických metód na výpočet vzájomných vzťahov medzi ordinálnymi premennými, ktoré sú založené na porovnávaní hodnôt premenných medzi jednotkami v súbore. Konkrétne porovnávanie hodnôt medzi jednotlivými respondentami, kde sa porovnáva respondent 1 s respondentom 2, atď. Pri tomto porovnávaní sa hľadá vzájomná zhoda/nezhoda.

Goodmanova – Kruskalova gamma (Goodman and Kruskal’s gamma – G)

Softvér PSPP používa skratku pre tento koeficient GAMMA a je založená na porovnávaní hodnôt premennej v prípade po sebe nasledujúcich jednotiek v súbore. Nadobúda hodnoty od – 1 po 0 alebo od 0 po 1.

Kenadallovo tau b (Kendall’s tau b – τ)

Počíta sa na rovnakom princípe ako hore uvedená gamma, no z menovateľa nevylučuje páry so spriahnutým poradím. PSPP používa skratku pre tento koeficient BTAU. Výsledok u obidvoch tau nadobúda hodnoty v intervale -1 až 0, resp. 0 až 1.

Kenadallovo tau c (Kendall’s tau c – τ)

Princíp výpočtu je rovnaký ako v prípade Kenadallovo tau b a v menovateli je aj počet jednotiek vo výbere. Výsledok u obidvoch tau nadobúda hodnoty v intervale -1 až 0, resp. 0 až 1. PSPP používa skratku pre tento koeficient CTAU.

Spearmanovo rho (Spearman correlation)

Je korelačný koeficient, ktorý je založený na poradí premenných. Na rozdiel od Pearsonovho koeficientu ho môžeme aplikovať aj na nie normálne rozložené (distribuované) dáta a dokáže zachytiť iný než len lineárny vzťah medzi premenenými.  Zároveň nie je tak citlivý na extrémne hodnoty (outliers) ako Pearsonov korelačný koeficient. PSPP používa skratku pre tento koeficient CORR a nadobúda hodnoty od -1 po 0 v prípade nepriamej závislosti a od 0 po 1 v prípade priamej závislosti.

Príklad č. 2. Študenti body a pamäť

Študenti boli požiadaní aby posúdili kvalitu podnikateľského zámeru opísanú v podnikateľskom pláne a pridelili mu body od 0 po 10. Podnikateľský plán bol opísaný 25 charakteristikami ako cena, súčasná konkurencia, vzhľad  atď. avšak študenti okrem nadpisu obsah vlastností hneď nevideli, ale mohli si na ne kliknúť a potom sa im objavil obsah. Takmer všetky charakteristiky boli opísané pozitívne, avšak v 3 najdôležitejších charakteristikách ( ako napr. ziskovosť, alebo doba návratnosti ) z 25 boli slabé miesta tohto plánu. Skúsený manažér by preto podnikateľský plán hodnotil negatívne. Zaujíma nás či počet otvorených podnikateľských charakteristík súvisí s celkovým hodnotením podnikateľského plánu. Očakávame, že čím viac podnikateľských charakteristík si študent otvoril a videl ich obsah, tým realistickejší obraz o pláne získal a odhalil jeho slabé miesta, a preto ho hodnotil nie príliš pozitívne. Hypotézy si stanovíme nasledovne:

H₁ Počet otvorených podnikateľských charakteristík v business pláne je v negatívnom vzťahu s celkovým hodnotením podnikateľského plánu.

H₀ Počet otvorených podnikateľských charakteristík v business pláne nesúvisí s celkovým hodnotením podnikateľského plánu.

Riešenie:

To akú štatistickú metódu použijeme na overenie vzájomných vzťahov v tomto prípade závisí od ako sú dáta rozložené (normálne rozloženie alebo nie normálne rozloženie našich dát). Parametrický test štatistickej významnosti robíme pomocou Pearsonovho korelačného koeficientu a používame ho len vtedy ak majú premenné normálne rozdelenie. Ten je uvedený v programe PSPP v menu Analyzovať(Analyze) ako Bivariate Correlation. V prípade, ak rozdelenie našich dát nie je normálne, alebo ho nevieme overiť, musíme používať neparametrické testy korelačného koeficientu (Pacáková, 2015, str. 220), ktoré sú uvedené vyššie. Čiže postup práce bude nasledovný:

1. krok – Overenie normality rozloženia dát
2. krok – Podľa toho ako sú dáta rozložené aplikujeme nasledovnú metódu: A) ak sú dáta rozložené normálne použijeme Pearsonov korelačný koeficient. B) ak dáta nie sú rozložené normálne použijeme Kendallovo tau. Môžeme použiť aj Spearmanovo rho a vysoký počet kategórií u premennej Počet otvorených charakteristík nám umožňuje teoreticky uvažovať s touto premennou ako s intervalovou a potom môžeme použiť aj koeficient Eta.

Postup:

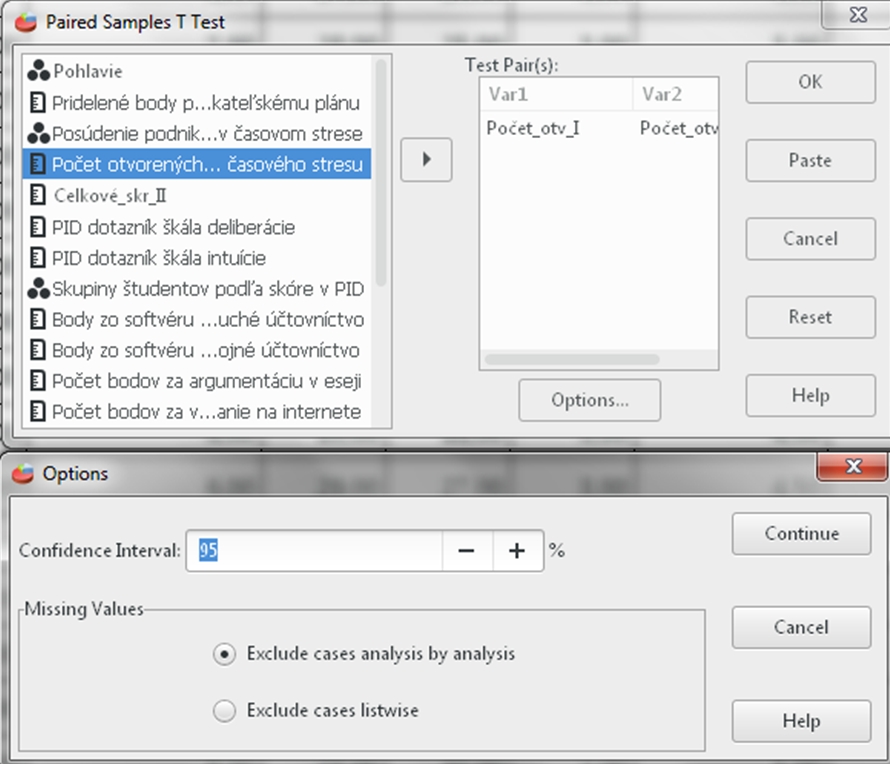
1. Krok: Overenie normality rozloženia dát.

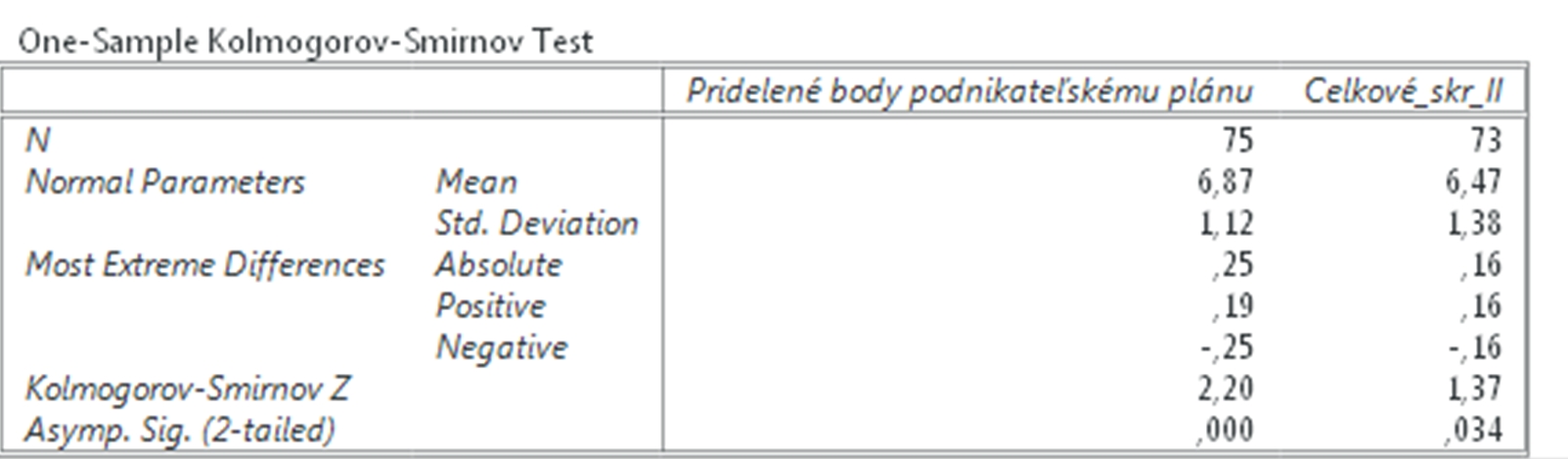
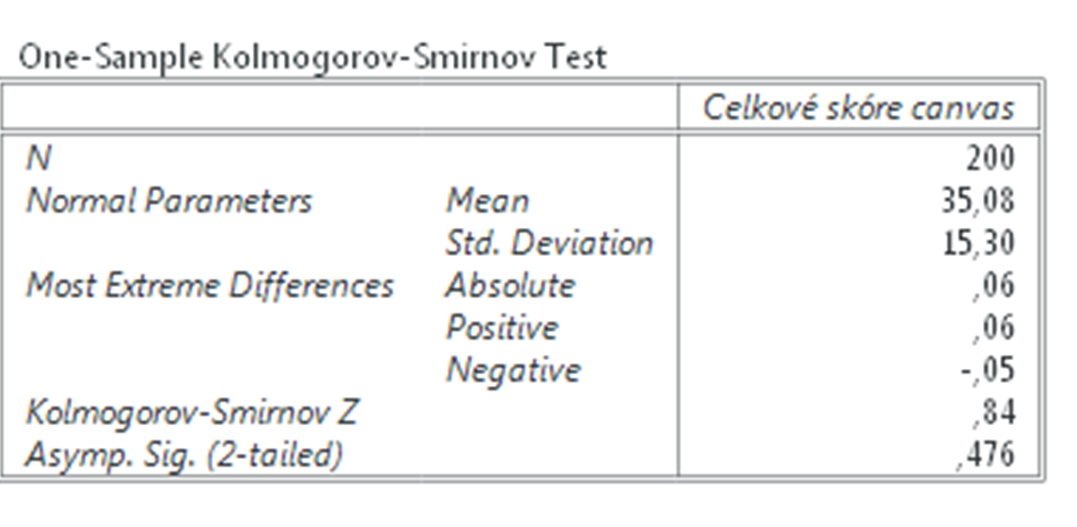
Na overenie normality rozoloženia dát použijeme Kolmogorov Smirnovov test, ktorý sa nachádza v neparametrických štatistikách. Klikneme na Analyzovať (Analyze), potom na Neparametrické štatistiky (NonParametric Statistics) a vyberieme 1 výberový K – S (1Sample K – S), čo je skratka pre Kolmogorov – Smirnovov test.  Následne vyberieme premenné Počet_otv_II (čo je počet otvorených podnikateľských charakteristík bez časového stresu) a Celkové_skr_II (celkové skóre, ktoré študenti pridelili podnikateľskému plánu od 0 po 10) a dole zvolíme Test Distribúcie (Test Distribution). V našom prípade vyberieme Normálne rozloženie (Normal). Na záver klikneme OK.

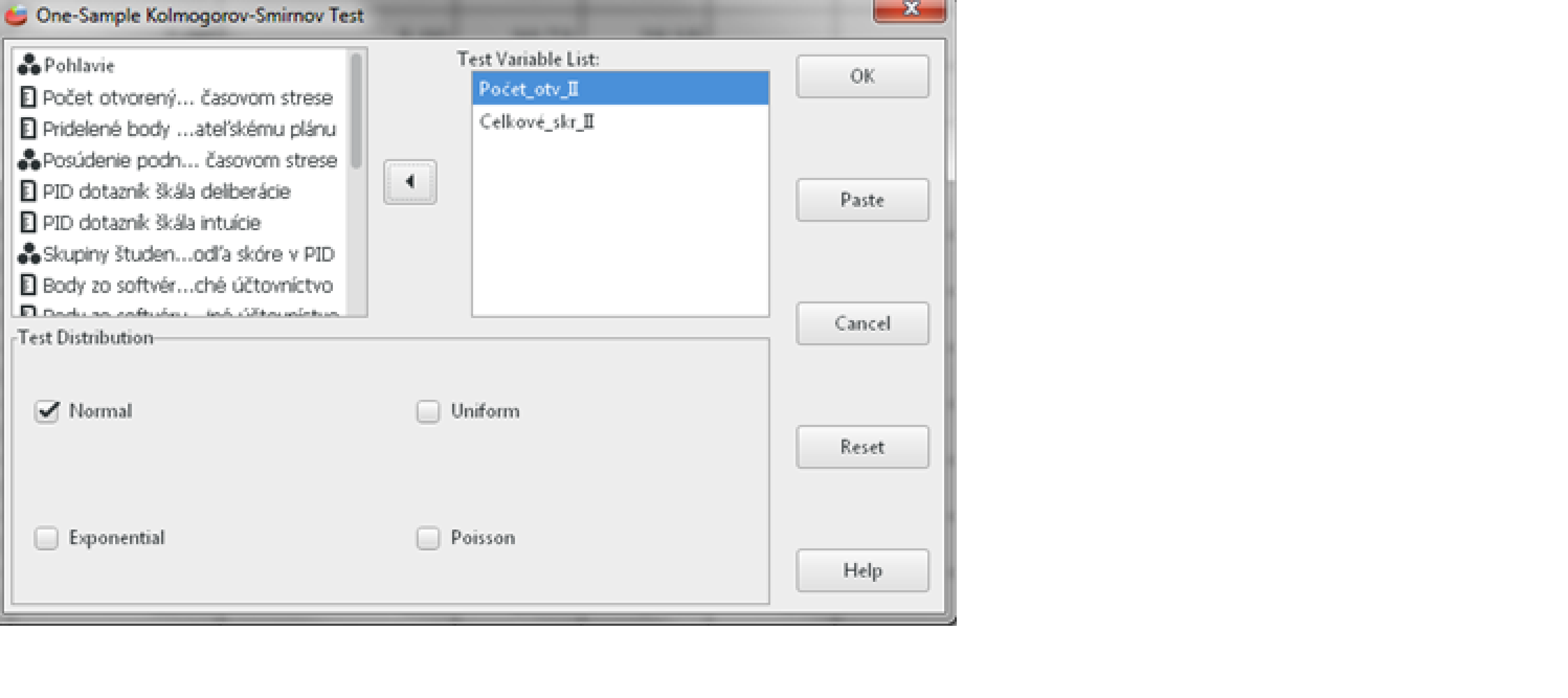
Obr. 1 Sprievodca overením normality rozloženia dát pomoc Kolmogorovho-Smirnovho testu

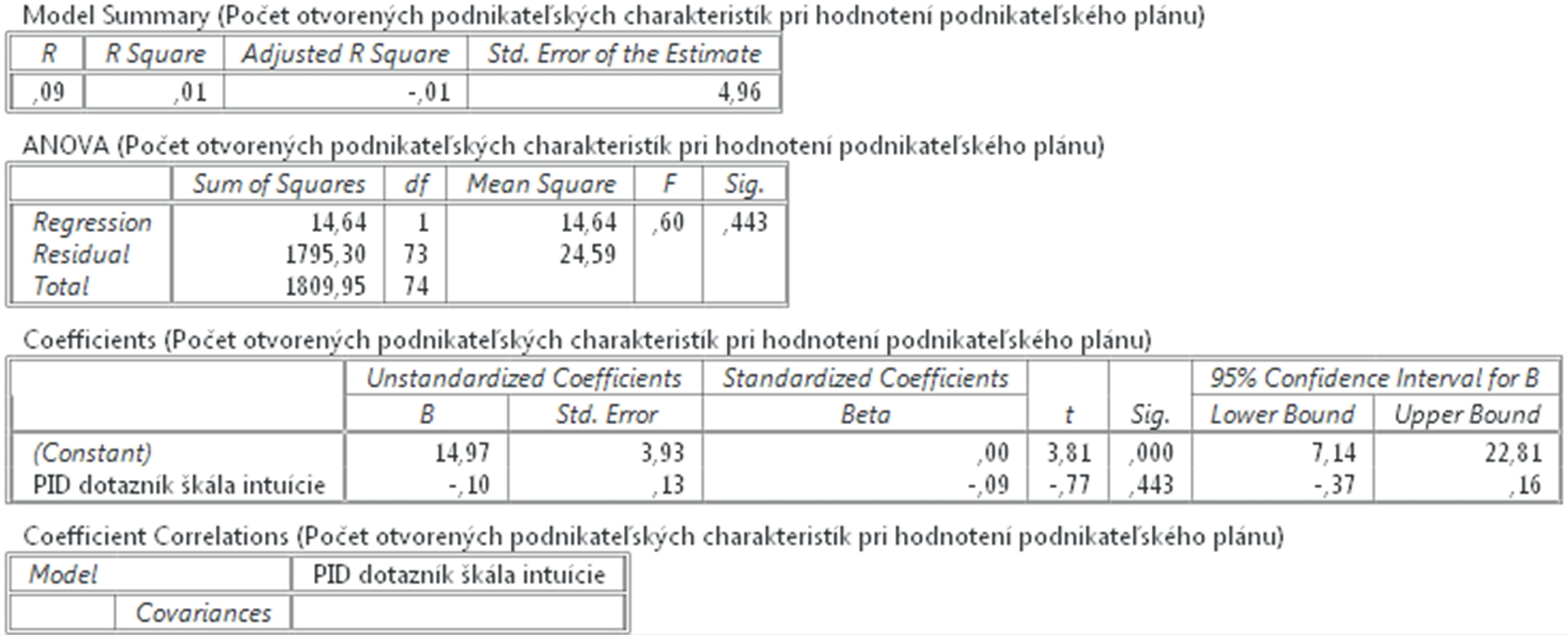
Výsledkom je tabuľka s opisnými charakteristikami a s výsledkami Kolmogorovho-Smirnovho testu uvedenými v posledných dvoch riadkoch.  Čiže ak je hladina významnosti v poslednom riadku nižšia než 0,05, potom sú výsledky nie normálneho rozloženia štatisticky významné. Čiže ak sú nižšie než 0,05, potom dáta nie sú rozložené normálne a nemôžeme použiť Pearsonov korelačný koeficient. Ako vidíme pri premennej Celkové skóre, tu je koeficient nižší než 0,05, teda hodnoty premennej nie sú rozložené normálne. Hoci pri premennej Počet otvorených podnikateľských charakteristík je mierne nad 0,05, stále je veľmi blízko a preto musíme použiť neparametrické testy na meranie vzájomnej závislosti premenných.

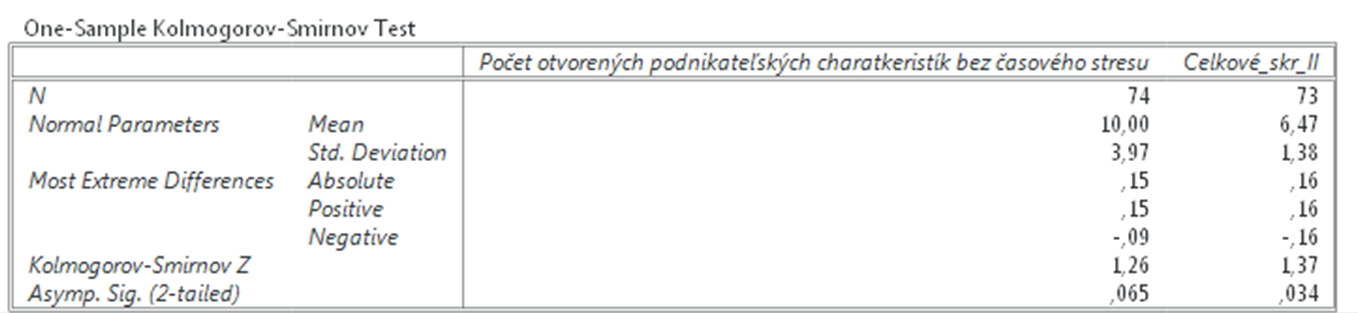
Obr. 2. Výsledok testu Kolmogorov-Smirnov Test normality rozloženia dát

2 krok: Výber vhodného testu na skúmanie vzťahov medzi premennými.

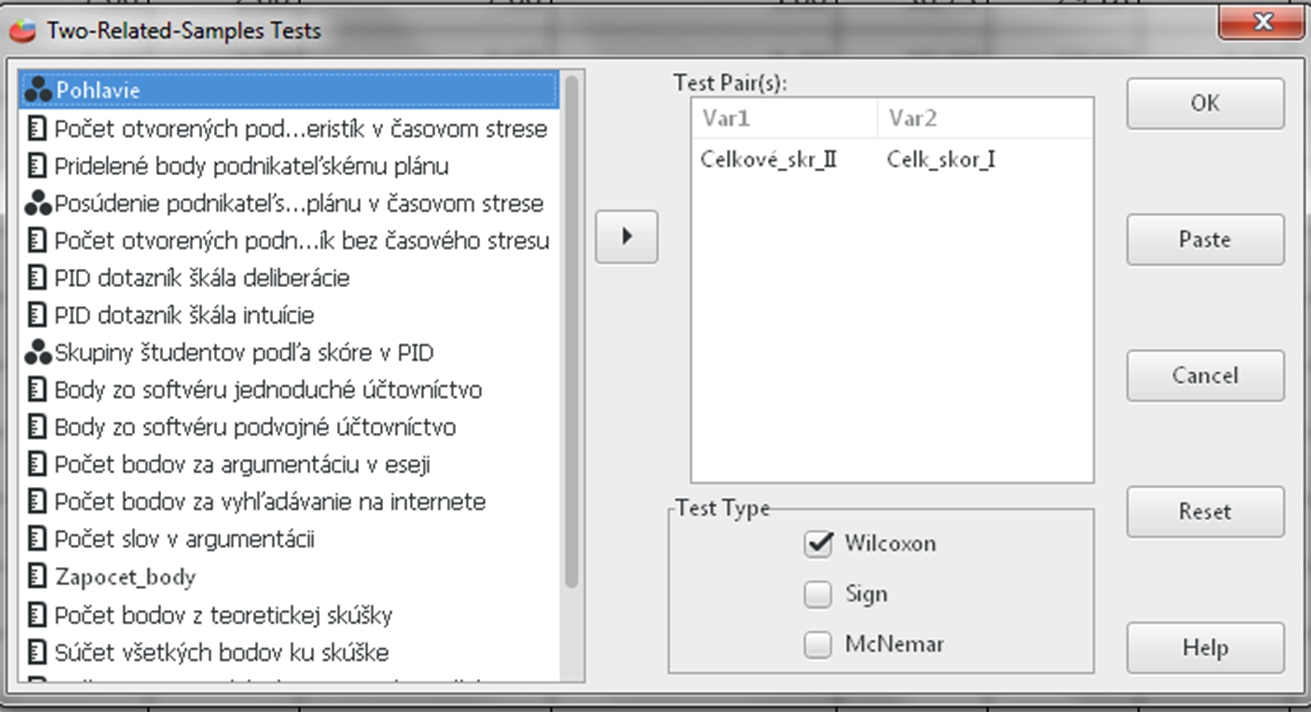
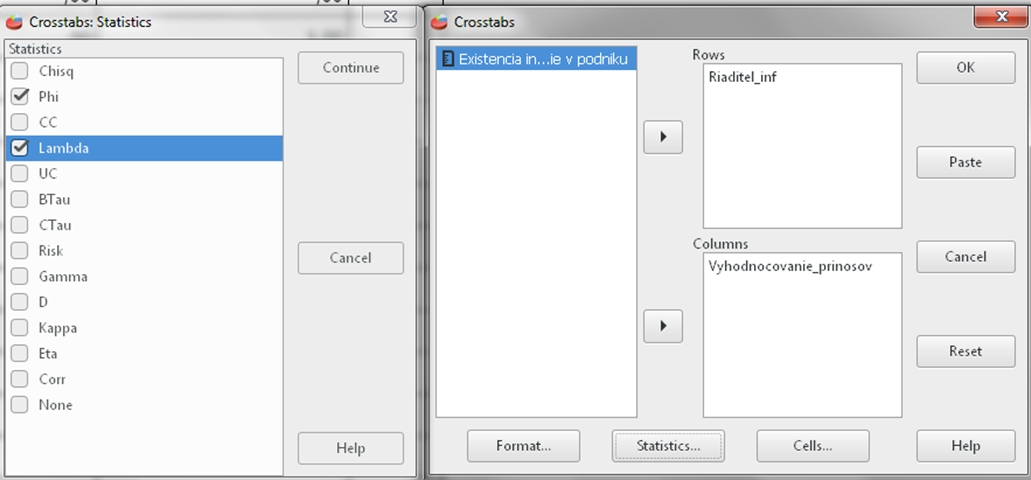
Na základe výsledkov Kolmogorovho-Smirnovho testu vieme, že dáta nie sú rozložené normálne, a preto nemôžeme použiť Pearsonovu koreláciu. Použijeme Kenallovo tau. To sa nachádza v Analyzovať (Analyze), potom klikneme na Opisné štatistiky (Descriptive Statistics) a vyberieme Krížové tabuľky (Crosstabs). Vyberieme nasledovné dve premenné: Počet_otv_II (čo je počet otvorených podnikateľských charakteristík bez časového stresu) a Celkové_skr_II (celkové skóre, ktoré študenti pridelili podnikateľskému plánu od 0 po 10) V dialógovom okne si dole otvoríme Štatistiky (Statistics) a vyberieme si, konkrétnu štatistickú metódu, ktorú chceme spustiť. V našom prípade je to Kendallovo Tau b aj c, označené ako BTau a CTau, koeficent Eta a Spearmanovu koreláciu označenú Corr. Následne klineme OK.

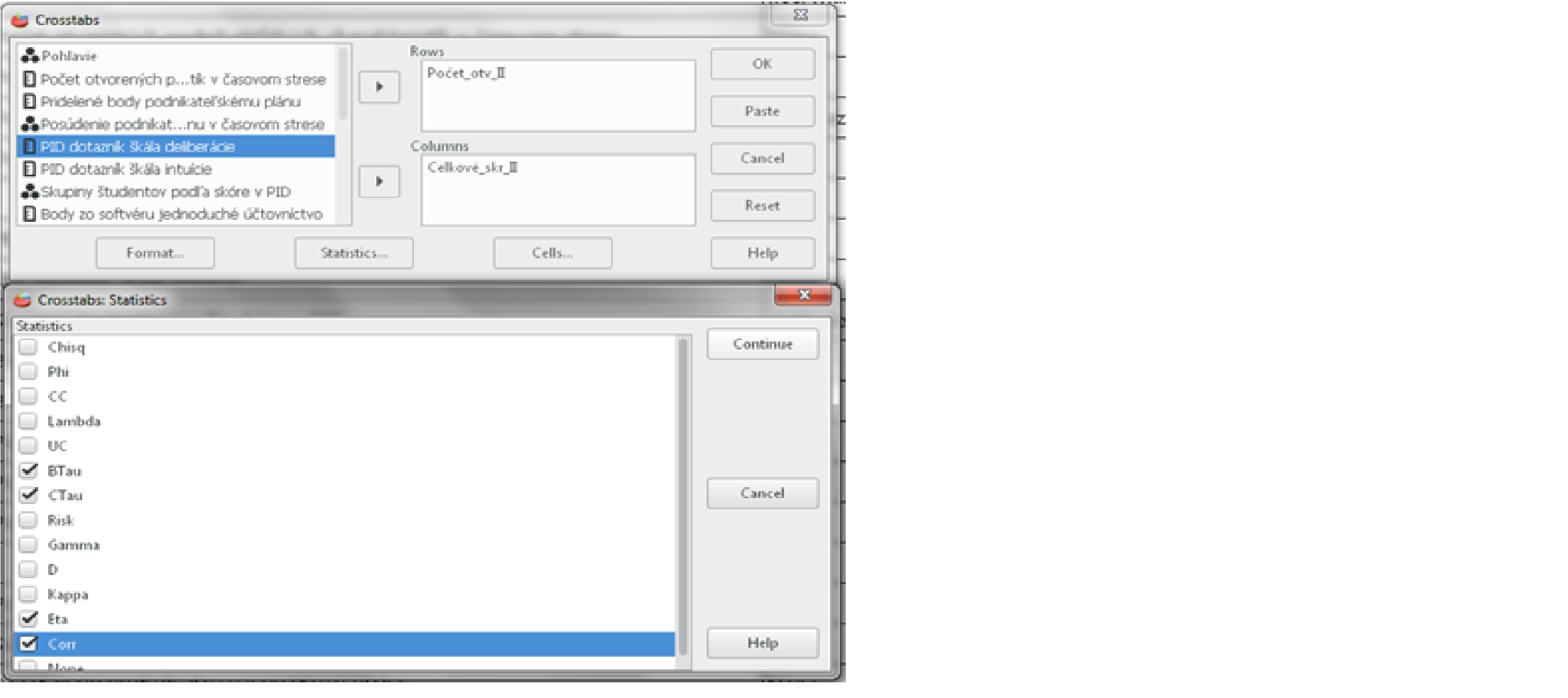
Obr. 3.  Sprievodca Spearmannovou koreláciou a Kendallovým tau a koeficientom Eta.

Výsledok a interpretácia:

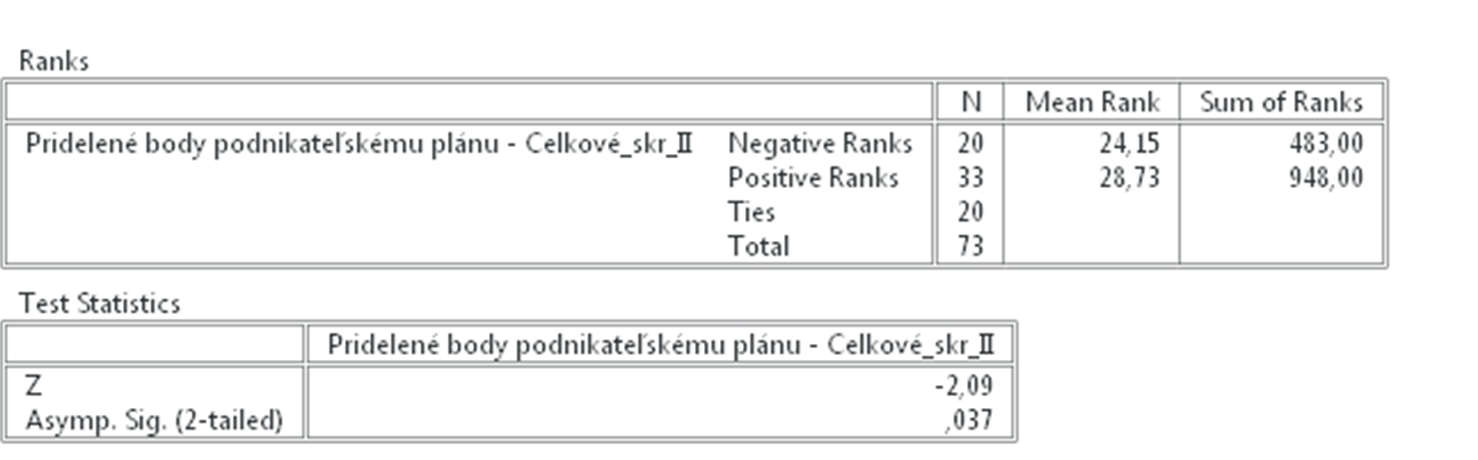
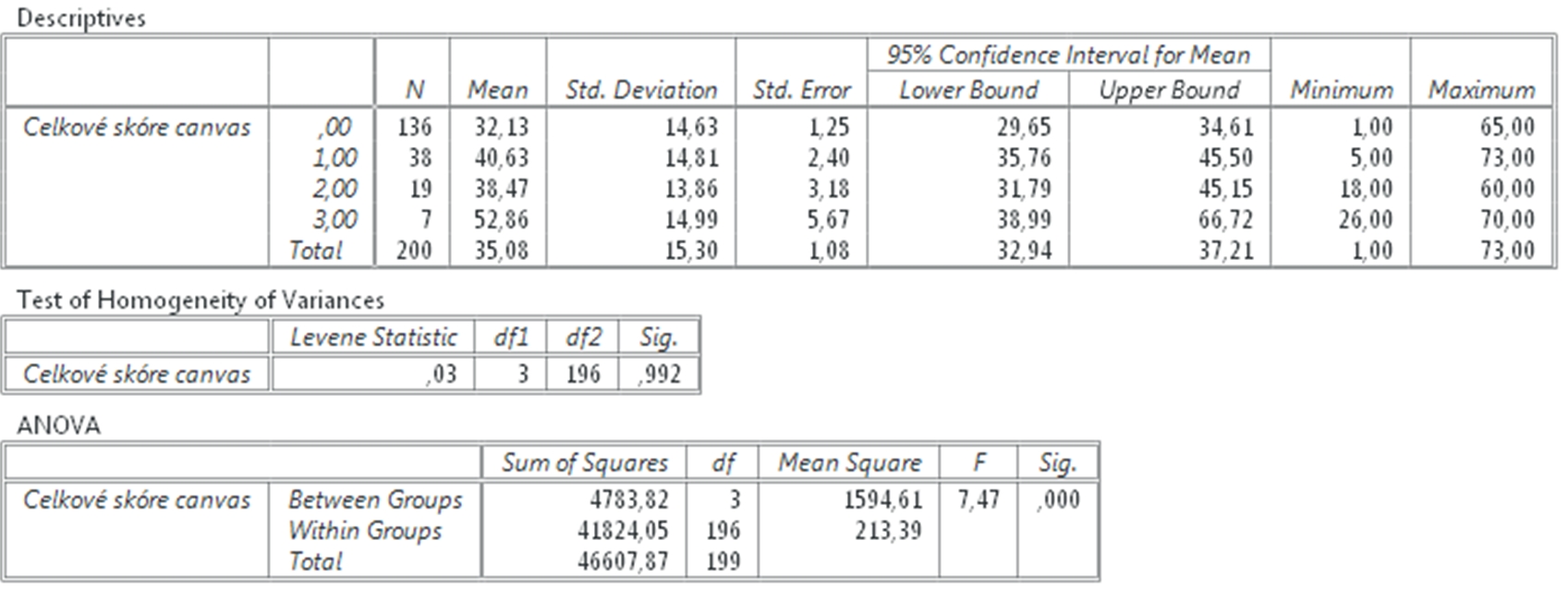
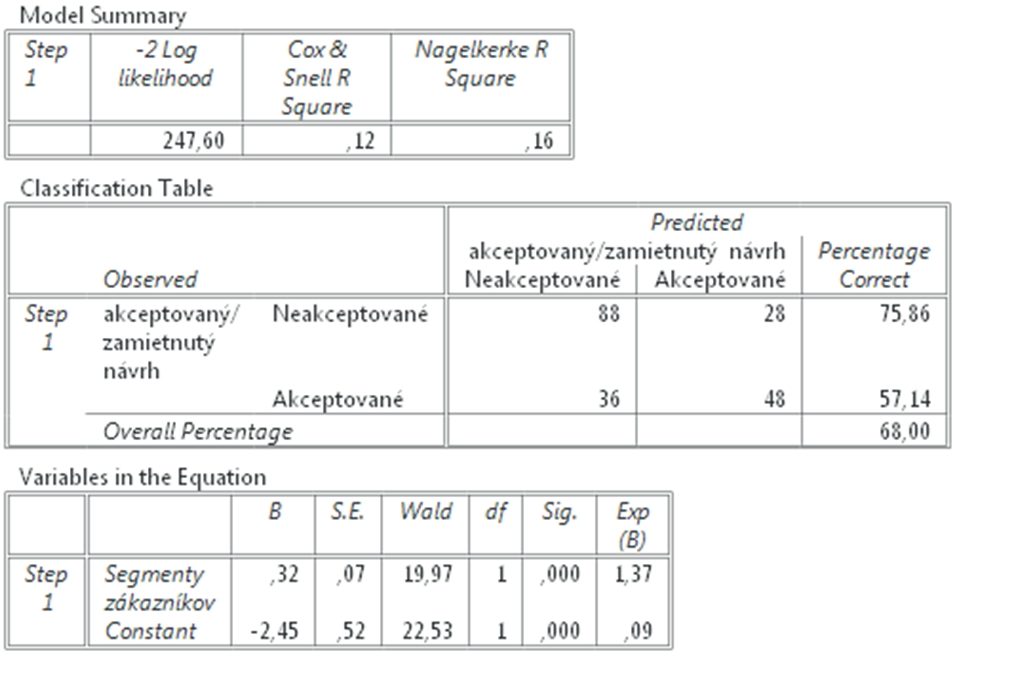
Výsledkom sú dve tabuľky, ktorých obsah si v krátkosti opíšeme. Hodnoty Kenallovho tau – b a tau-c sú 0,18 a 0,17, Spearmanova korelácia je 0,23 a program PSPP zobrazil aj výsledky Pearsonovej korelácie = 0,2. Výsledky sa odlišujú nakoľko každá štatistická metóda je založená na inom vzorci, avšak hodnoty sú podobné. Ak si máme vybrať, ktoré výsledky budeme uvádzať, potom použijeme pravidlo, ktoré hovorí, že reportujeme tú metódu, ktorej výsledok je najnižší.

Súčasne môžeme konštatovať, že nie sú vysoké (bližšie k 0 než 1) a teda vzájomný vzťah síce existuje, ale nie je veľmi silný. Koeficienty sú všetky pozitívne, čo znamená, že čím viac si študent podnikateľských charakteristík otvoril, tým vyššie skóre podnikateľskému plánu dal. Čo sa týka koeficientu Eta ak by sme uvažovali o celkovom skóre podnikateľského plánu ako závislom na počte otvorených podnikateľských charakteristík, potom je koeficient Eta = 0,42, čo je už pomerne silný vzájomný vzťah. Ak umocníme koeficient eta na druhú mocninu, tak dostaneme 17,64%  a môžeme konštatovať že 17,64%  variability z celkového skóre pre podnikateľský plán závisí od počtu otvorených podnikateľských charakteristík. V hypotéze H₁ sme tvrdili, že premenné budú v negatívnom vzájomnom vzťahu, čo sa nám nepotvrdilo, a preto hypotézu H₁ zamietame a prijímame hypotézu H_0.

Obr. 4. Výsledok Kenallovho tau, Spearmanovej korelácie a koeficientu Eta.

Reportovanie výsledkov:

Počet otvorených podnikateľských charakteristík bez časového stresu súvisí s celkovým hodnotením podniku len mierne Kenallove tau c = 0,17.

 Spracoval Róbert Hanák, Február 2016

Vzťahy medzi nominálnymi premennými meriame týmito štatistickými metódami:

Koeficient phi (phi coeficient – φ)

Program PSPP má pre tento označenie PHI.  Používa sa na skúmanie vzťahov medzi dvoma dichotomickými premennými, napríklad absolvoval školenie (áno = 1, nie = 0), alebo pohlavie (muž = 0, žena = 1). Výsledok výpočtu je veľmi podobný korelačnému koeficientu a nadobúda hodnoty 0 – žiadna závislosť premenných až 1 – úplná vzájomná závislosť.

Cramérovo V (Cramér’s V)

Mareš a kolektív (2015) uvádzajú, že tento koeficient sa používa na meranie vzťahov u dichotomickej premennej a premennej, ktorá nadobúda viacero kategórii než dve (napr. vzdelanie: záklané = 0, stredoškolské odborné = 1, stredoškolské s maturitou = 2, vysokoškolské bakalárske  =1, atď. ). Môžeme ho použiť aj u dvoch premenných, ktoré obidve majú viac kategórií než dve. Rovnako ako u koeficientu PHI výsledok nadobúda hodnoty od 0 – žiadny vzájomný vzťah medzi premennými, až po 1 – úplný vzájomný vzťah. Softvér PSPP, nemá samostatný príkaz na výpočet, ale vypočíta Cramérovo V spolu s koeficientom PHI.

Goodmanova – Kruskalova lambda (Goodman and Kruskal’s lambda -λ)

Na rozdiel od predchádzajúcich dvoch koeficientov Goodmanova – Kruskalova lambda umožňuje merať aj predpokladaný príčinný vzťah medzi nezávislou a závislou premennou. Ak sa snažíme predpovedať jednu premennú pomocou druhej, potom lambda nám vyjadruje zníženie chyby predpovede druhej premennej ak poznáme hodnotu prvej.  Ritomský a Hankes (1994, str. 138) ju definuje ako: „relatívne zníženie pravdepodobnosti chybnej predikcie jednej premennej  pri znalosti hodnoty druhej premennej.“ Nadobúda hodnoty od 0 po 1. Ak nám vyjde hodnota napríklad 0,35, a toto číslo prevedieme na percentá = 35%, potom môžeme konštatovať, že sme znížili pravdepodobnosť chyby o 35%.

Koeficient Eta (Eta coeficient)

Tento koeficient meria vzťahy medzi nominálnou premennou a intervalovou. Rovnako ako hore uvedené koeficienty aj Eta nadobúda hodnoty od 0 do 1, kde hodnoty blízke nule znamenajú minimálnu, respektíve žiadnu závislosť a 1 znamená úplnú závislosť. Softvér PSPP používa skratku pre tento koeficient ETA. Rimančík (2007) uvádza, že druhá mocnina koeficientu Eta sa označuje η² udáva aký podiel variability intervalovej premennej vysvetľuje nominálna premenná.

Príklad.

Zadanie: Zistite či existuje vzájomná závislosť medzi tým existenciou pracovnej pozície: riaditeľ informatiky a vyhodnocovaním prínosov informačných technológií.

 Riešenie:

V súbore s názvom Riaditeľ IT.sav  sú uvedené výsledky za 225 skutočných podnikov v SR, ktorí uviedli či majú pozíciu riaditeľa informatiky (áno = 1, nie = 0) a či a či vyhodnocujú prínosy informačných technológií (áno = 1, nie = 0). Pretože obe premenné sú dichotomické, tak musíme na vypočítanie vzájomnej súvislosti medzi nimi použiť koeficient PHI. Ďalej predpokladáme, že medzi premennými existuje príčinná súvislosť, konkrétne, že ak existuje pracovná pozícia riaditeľa informatiky, tak ten potom vyhodnocuje prínosy informačných technológií pre podnik. A preto použijeme aj Goodmanovu – Kruskalovu lambdu ako druhú štatistickú metódu na otestovanie našich hypotéz, ktoré sme si stanovili nasledovne:

H₁: Pozícia riaditeľa informatiky priamo ovplyvňuje vyhodnocovanie prínosov informačných technológií.

H₀: Pozícia riaditeľa informatiky neovplyvňuje vyhodnocovanie prínosov informačných technológií.

Klikneme Analyzovať (Analyze), potom Opisné štatistiky (Descriptive Statistics) a Krížové tabuľky (Crosstabs). Vyberieme nasledovné dve premenné: do okna Riadky (Rows) presunieme premennú Riaditel_inf a do okna Stĺpce (Columns) premennú Vyhodnocovanie_prinosov. V dialógovom okne si dole otvoríme Štatistisky (Statistics) a vyberieme si Koeficient Phi – Phi a Goodmanovu – Kruskalovu lambdu. Potom klikneme Ok.

Obrázok č. 1. Sprievodca pre koeficient PHI a Goodmanovu – Kruskalovu lambdou (Lambda)

Výsledok:

Obrázok č. 2. Vzájomná závislosť medzi pozíciou riaditeľa informatiky a vyhodnocovaním prínosov informačných techonológií podniku počítanej pomocou koeficientu phí (PHI) a Goodmanovou – Kruskalovou lambdou.

Interpretácia:

Koeficient fí (Phi) ako aj Cramérovo V je 0,36. Hoci koeficient nie je zanedbateľný je pomerne malý, čiže súvislosť existuje, nie je však silná. Na otestovanie hypotéz,  že riaditeľ informatiky znamená následne vyhodnocovanie prínosov informačných technológií sme použili Goodmanovou – Kruskalovou lambdou kde kde λ = 0,19, p = 0,11. Hodnota Lambdy je tiež pomerne nízka a súčasne nie je štatisticky významná, nakoľko p je väčšie než hodnota 0,05.  Na základe týchto výsledkov zamietame hypotézu H₁ a príjmame hypotézu H₀. Každopádne musíme konštatovať, že určitý vplyv tam existuje.

Reportovanie výsledkov:

Pozícia riaditeľa informatiky automaticky neznamená, že podnik bude vyhodnocovať prínosy informačných technológií. Vzájomná závislosť meraná Goodmanovou – Kruskalovou lambdou kde λ = 0,19, p = 0,11 nepreukázala štatisticky významný príčinný vzťah.

Spracoval Róbert Hanák,  13 Máj 2016

Binárna logistická regresia je špecifický typ regresnej analýzy, pri ktorej je závislá premenná v nominálnej forme a nadobúda dve hodnoty, zvyčajne kódované ako  0 alebo 1. Nezávislá premenná môže byť ordinálna aj intervalová. Aby sme dokázali určiť, či nezávislá premenná spôsobuje, že závislá premenná nadobudne jeden alebo druhý stav (sa stane nulou alebo jednotkou), potom musíme pracovať s pravdepodobnosťami. Preto aj vzorec na vzťah medzi závislou premennou (Y) a nezávislou (X) je odlišný od vzorca, ktorý sa používa pri lineárnej regresii. Matematicky vyjadrený vzťah medzi premennými je nasledovný:

Kde: e – je základ prirodzeného algoritmu.

Ostatné premenné v rovnici sú rovnaké ako pri lineárnej regresii, ktoré opisujeme v inom okne web stránky.

1 úloha: V databázovom súbore Príklad č. 7 s názvom Canvas metódy a startup.sav sú uvedené opisné charakteristiky 200 podnikateľských zámerov, kde začínajúci podnikatelia žiadali finančné prostriedky od nezávislých investorov na rozvoj ich podnikateľského zámeru. Pri prvotnom hodnotení špecializovaní poradcovia hneď vylúčili 116 podnikateľských zámerov ako nekvalitných a 84 akceptovali na ďalšie hodnotenie. Podnikateľský zámer bol teda odmietnutý (kódovaný ako 0) alebo akceptovaný (kódovaný 1). Canvas metóda je podnikateľský  postup, pomocou ktorého sa opisuje podnikateľský zámer v konkrétnych kategóriách. Hodnotia sa ako dobre sú definovaný zákazníci, ako sa budú získavať príjmy, aké zdroje budú potrebné a mnohé iné charakteristiky, ktoré sumárne opisujú podnikateľský zámer. Jednou z kategórií Canvas sú segmenty zákazníkov (Customer Segments), ktoré boli merané na škále od skóre 0 (nemá definovaných zákazníkov) po skóre 10 (zákazníci sú podrobne, jednoznačne a dôkladne definovaní). Segmenty zákazníkov môžu byť opísané veľmi dôkladne a podrobne a preto pri hodnotení dostane vysoké skóre, alebo môže byť opísaný nedostatočne a povrchne a  skóre je potom nižšie.

V našej analýze nás zaujíma či tie podnikateľské zámery, kde boli opísané Segmenty zákazníkov dôkladne a podrobne (mali  lepšie definované segmenty zákazníkov a teda vyššie skóre) mali vyššiu pravdepodobnosť byť akceptované  oproti tým, ktoré mali skóre v Segmentoch zákazníkov nízke.

Riešenie:

V našom príklade je závislá premenná dichotomická (akceptovaný verzus odmietnutý) a nezávislá premenná (skóre v segmentoch zákazníkov) je škálová (môže nadobúdať hodnoty 0 až 10). Zvolíme preto binárnu logistickú regresiu.

Otvoríme si príklad č. 7 Canvas metódy a startup. Následne klikneme na Analyzovať (Analyze) vyberieme si Regresiu (Regression) a z dvoch dostupných možností si vyberieme Binárnu Logistickú (Binary Logistics). V sprievodcovi binárnou logistickou regresiou musíme si definovať závislú premennú. V našom prípade je to premenná akceptovane_neakceptovane. Nezávislá premenná – tá ktorá ovplyvňuje závislú premennú je Segementy zákazníkov, označená ako Segment. Ďalej klikneme na Možnosti (Options) a v sprievodcovi zaškrtneme nastavenia Intervalov spoľahlivosti (confidence intervals). Softvér PSPP v niektorých prípadoch požaduje iné nastavenia iterácií, než je predvolené a bez tejto zmeny nevypočíta výsledok. Preto počet iterácií výpočtu zvýšime na 21 (Maximum iterations), a Clasification cutoff zvýšimi na 0,51 a zaškrtneme políčko Konštanta v modeli (Include constant in model). Zvýšenie o jednu jednotku v oboch hore uvedených príkladoch sme zaklikli preto, aby nás softvér pustil ďalej a vypočítal výsledok. Klikneme na Pokračovať (Continue) následne OK.

Obr. 1 Sprievodca binárnou logistickou regresiou

Výsledky: Výsledkom je päť tabuliek a my budeme interpretovať údaje z posledných troch.

Obr. 2  Výsledok binárnej logistickej regresie, posledné 3 tabuľky.

Tretia tabuľka je sumárny model (Model Summary), ktorá uvádza koľko variancie model vysvetľuje. Výsledok je vypočítaný dvoma metódami, kde Cox & Snell R Square = 0,12 a Nagelkerke R Square = 0,16, čo znamená že model vysvetľuje podľa Cox & Snell 12% variability a podľa Nagelkerke 16% variability.

Posledná, piata tabuľka je najdôležitejšia. Vysvetlíme si čo znamenajú jednotlivé výsledky. Stĺpec Wald nám hovorí či b koeficient pre prediktor je štatisticky významne odlišný od nuly. V našom prípade teda či predpovedá výsledok výberu. Vidíme, že Wald(ovo) z rovné 19,97 a p < 0,001. Hladina významnosti v našich výsledkoch je oveľa nižšie než všeobecne akceptovaná podmienka p <0,05.

Exp(B) je exponenciálne B, ktoré vyjadruje zvýšenie pomeru šancí (odds ratio) výskytu  udalosti pri zvýšení hodnoty prediktora o jednotku. Pomer šancí (odds ratio) Field (2013, str. 880) definuje ako: „pomer šancí výskytu udalosti v jednej skupine v porovnaní s výskytom udalosti v druhej skupine.“ Field uvádza príklad, kde šanca výskytu určitej udalosti v jednej skupine je napríklad 4 a v druhej skupine je napríklad len 0,25, tak vzájomný pomer je 4/0,25 = 16.  Ak je je exponenciálne B Exp(B) rovné 1, pomer šancí v jednej aj v druhej je rovnaký a  potom zmeny prediktora nemajú žiaden vplyv. Ak je väčšie ako 1, potom zvyšovaním prediktora rastú šance na výskyt udalosti. Výsledok v našom prípade je Exp(B) = 1,37 teda ak zýšime hodnotu v nezávislej premennej o jednu 1 potom vzrastie pomer šancí byť akceptovaný na 1,37.

Interpretácia:

Dosiahnuté skóre v Segmentoch zákazníkov  je štatisticky významný prediktorom pre akceptáciu podnikateľského plánu investormi, Wald(ovo) Z je  19,97 a p < 0,001, exponenciálne B  (Exp. B) = 1,37.  Model vysvetľuje R squared =  0,16 variability (Nagelkerke).

Spracoval Róbert Hanák, 5 Júl 2015

Úvod
Pri regresnej analýze skúmame vzťah medzi dvoma, prípadne medzi viacerými premennými. Predpokladáme, že 1 premenná závisí od druhej premennej, ktorá ju ovplyvňuje. Tých premenných, ktoré ovplyvňujú môže byť aj viacero, nielen jedna. Premenná, ktorá závisí od inej alebo od viacerých sa nazýva závislá, po anglicky dependend variable (DV, v regresnej rovnici sa označuje Y). Tá premenná, alebo ak ich je viac, tak tie premenné, ktoré ju ovplyvňujú sa nazývajú nezávislé premenné, independent variable (IV, v regresnej rovnici označené X) alebo aj prediktor. Ak je medzi premennými lineárny vzťah, potom nám regresná analýza umožní presne matematicky vyjadriť tento vzťah. Napr. ak zvýšime premennú X (nezávislú premennú, IV) o 1 jednotku, tak sa druhá premenná (závislá, DV) zvýši o 1,25. Matematický vzťah premenných v regresnej rovnici sa vyjadruje nasledovne:
Pre 1 nezávislú premennú:
Y = b0+ b1* X + e
Pre viac nezávislých premenných:
Y = b0+ b1* x1 + b2* x2 + … bn* xn + e
kde: Y – je závislá premenná, X je nezávislá premenná(é), b0 je bod, kde regresná priamka pretína osu Y, b1 je regresný koeficient, ktorý určuje smer priamky, e je chyba merania.

Zadanie:

Príklad č. 2 Študenti body a pamäť
Študenti boli požiadaní, aby posúdili v limitovanom čase do 3 minúť podnikateľský plán začínajúceho podniku, ktorý bol opísaný 25 charakteristikami ako napríklad súčasná konkurencia, ziskovosť, vzhľad produktu, cena a ostatné. Študenti videli len názov ale ich obsah nevideli, a museli vždy kliknúť na políčko napr. ziskovosť, ak chceli vedieť aká konkrétna je ziskovosť v tomto podnikateľskom pláne. Študenti zároveň vyplnili dotazník PID, ktorý meria preferenciu k intuícii a uvažovaniu – deliberácii pri rozhodovaní.
Vypočítajte či má preferencia k intuícii vplyv na počet otvorených podnikateľských charakteristík pri posudzovaní podnikateľského plánu.
Predpokladáme, že študenti, ktorí sa v rozhodovaní spoliehajú na intuíciu, dokážu prijímať rozhodnutia s menším počtom informácií než rozvažujúci študenti, ktorí viac hĺbajú nad problémom (Betsch, 2004). Teda čím viac bude študent intuitívnejší, tým menej informácií bude potrebovať pri rozhodovaní a otvorí si menej charakteristík podnikateľského plánu.
Hypotézy sme si stanovili nasledovne:
H1: Dosiahnuté skóre v škále intuícia v dotazníku PID je štatisticky významným prediktorom počtu otvorených podnikateľských charakteristík pri posudzovaní podnikateľského plánu.
H0: Dosiahnuté skóre v škále intuícia v dotazníku PID nie je štatisticky významným prediktorom počtu otvorených podnikateľských charakteristík pri posudzovaní podnikateľského plánu.

Riešenie:
Na riešenie použijeme lineárnu regresnú analýzu, ktorej postup v programe PSPP je nasledovný. Klikneme Analyzovať (Analyze) potom na Regresia (Regression) a vyberieme Lineárna regresia (Linear). Ďalej klikneme na Štatistiku (Statistics) a zaškrtneme všetky políčka. Ich obsah si vysvetlíme v časti výsledky.
Pri regresii musíme správne nastaviť jednotlivé parametre analýzy ako aj premenné a ich miesto v analýze. V dialógovom okne určíme najprv závislú (Dependent variable – DV) a nezávislú premennú (Independent variable – IV). V našom prípade nás zaujíma ako preferencia k intuícii ovplyvňuje počet otvorených podnikateľských charakteristík pri posudzovaní podnikateľského plánu. Teda preferencia k intuícii uvedená ako: PID_intu bude nezávislá premenná (Independent variable) a počet otvorených podnikateľských charakteristík uvedený ako: Počet_otv_I bude závislá premenná (Dependent variable). Počet otvorených závisí od intuície študenta. Ďalej v dialógovom okne v ľavej časti dole Štatistika(Statistics) zaškrtneme všetky políčka.

Obr. 1. Sprievodca regresnou analýzou

Výsledky:
Program PSPP vytvorí štyri tabuľky, ktoré si podrobne opíšeme.

Obr. 2. Výsledok lineárnej regresie

Prvá tabuľka s názvom Sumarizácia Modelu (Model Summary) opisuje regresný model. Význam jednotlivých koeficientov je nasledovný:
R je korelačný koeficient medzi počtom otvorených podnikateľských charakteristík a škálou intuície. V našom prípade je 0,09, čo je hodnota blízka nule. To znamená že medzi našimi premennými je len veľmi slabý vzťah.
R Square je koeficient determinácie. Je druhou mocninou korelačného R a vysvetľuje koľko percent variability závislej premennej Y – Počet otvorených podnikateľských charakteristík ovplyvňuje nezávislá premenná X – škála intuície. V našom prípade vidíme, že hodnota je veľmi nízka, rovná 0,01, teda 1%. Inými slovami, to ako intuitívni študenti sú, ovplyvnilo len 1 % z toho, koľko podnikateľských charakteristík si otvorili. 99% ovplyvňujú všetky ostatné faktory ako napríklad skúsenosť, sebaistota a iné.
Tabuľka ANOVA udáva ako dobre regresný model opisuje dáta. Posledné dva stĺpce uvádzajú hodnotu F = 0,6 a p = 0,44, čo je oveľa viac než akceptovaná hladina štatistickej významnosti p < 0,05.
V poslednej tabuľke sú uvedené koeficienty regresnej rovnice. V stĺpci B, Neštandardizované koeficienty (Unstandardized coefficients) je hodnota b0 = 14,97 a b1 = – 0,1. Z týchto koeficientov vieme zostaviť regresnú rovnicu, ktorá bude vyzerať nasledovne.
Y = 14,97 – 0,1* X, teda:
Počet otvorených podnikateľských charakteristík = 14,97 – 0,1* Skóre v škále intuícia (PID)
Ďalej je dôležité všimnúť si štandardizovaný koeficient (Standardized Coefficient) Beta, pre PID dotazník škála intuície, ktorý je 0,09 na hladine významnosti p = 0,44. Tá je vyššia než podmienka na prijatie hypotézy H1, ktorá je p < 0,05. V prípade, že máme len jednu nezávislú premennú, čo je aj náš prípad, potom je tento koeficient zhodný s korelačným koeficientom R v prvej tabuľke.
Intervaly spoľahlivosti pre B (95% Confidence Interval for B) sú CI [-0,37, 0,16] nám hovoria o tom kde sa bude pravdepodobne nachádzať hodnota hľadaného parametra. V rámci nášho intervalu sa nachádza 0, to znamená, že hľadaný parameter môže byť nulový.
Na základe hore uvedených výsledkov zamietame hypotézu H1 a prijímame hypotézu H0.
Poznámka:
V tomto príklade sme postupovali ako odporúčajú vedecké postupy, teda že mali sme určité teoretické predpoklady, podľa nich sme si stanovili hypotézy, navrhli výskum, zozbierali dáta na záver sme ich otestovali. Výsledky jednoznačne preukázali, že lineárny regresný vzťah medzi premennými neexistuje a intuícia meraná dotazníkom PID vôbec neovplyvňuje počet otvorených podnikateľských charakteristík. U začiatočníkov mohlo vyvolať sklamanie, že sme nepotvrdili hypotézu H1, avšak naše výsledky sú z vedeckého hľadiska rovnako hodnotné ako keby sme hypotézu potvrdili.

Reportovanie výsledkov:
Dosiahnuté skóre v škále intuícia merané dotazníkom PID nepredikuje počet otvorených podnikateľských charakteristík F(1, 73) = 0,6, p = 0,44. Vzájomný vzťah medzi premennými je takmer nulový a regresný model vysvetľuje len minimum variancie v počte otvorených ponikateľských charakteristík, koeficient determinácie R sq = 0,01 .

Spracoval Róbert Hanák, 7 September 2015

Dvojvýberový t – test s rovnosťou rozptylov

Zadanie: Porovnajte celkové skóre v intuícii u mužov a u žien.

Riešenie: Muži a ženy sú dve nezávislé skupiny v súbore, teda jedna druhú neovplyvňujú. Preto použijeme t – test pre dva nezávislé výbery (Independent samples T test). Mužov máme v súbore kódovaných v stĺpci pohlavie ako 1 a ženy ako 2. Pri porovnávaní skupín odporúčam stanoviť si hypotézy, ktoré nám pomôžu lepšie si ujasniť skúmanú otázku a vnímať problém exaktnejšie.

Čítať ďalej→

Korelačná analýza

Dáta na korelačnú analýzu nájdete v súbore s názvom:

korelačná analýza

Korelačná analýza je analýza závislosti dvoch premenných. Pomocou nej zisťujeme, ak sa mení 1 premenná, či to ovplyvňuje druhú premennú. Priama korelačná závislosť znamená, že ak rastie jedna premenná, potom aj druhá rastie. Napríklad čím viac kalórií prímam bez pohybu, tým viac vážim. Nepriama korelačná závislosť znamená, že keď jedna premenná rastie, potom druhá klesá. Napríklad u obéznych ľudí, čím viac športujú, tým menej vážia.

Výsledkom korelačnej analýzy je koeficient r, ktorý nadobúda hodnoty v intervale od -1 do +1. Mínus 1 znamená absolútnu nepriamu lineárnu závislosť, 0 znamená žiadnu závislosť a 1 znamená absolútnu priamu lineárnu závislosť. Inými slovami: čím je korelačný koeficient bližšie k 0, tým je vzťah medzi skúmanými premennými slabší, resp. neexistujúci. Naopak čím je bližšie k 1 alebo k -1, tým je vzťah medzi premennými silnejší. V praxi však tieto koeficienty takmer nikdy nenadobúdajú tieto hraničné hodnoty, ale sa pohybujú niekde v intervale. Preto my musíme hodnoty interpretovať sami. Hodnoty koeficientu korelácie   0,8 až 1 (-0,8 až -1) sú považované zvlášť silné, teda medzi premennými existuje veľmi silná vzájomná závislosť. Hodnoty 0,4 až 0,8 (-0,4 až -0,8) sú stredne silné a od 0 do 0,4 (-0,4 až 0 ) sú považované za slabé.

Zadanie:

Vypočítajte vzájomnú koreláciu medzi subškálami dotazníka PID deliberáciou a intuíciou.

Riešenie:

V súbore klikneme na Analyzovať (Analyze)→ Korelácia dvoch premenných (Bivariate Corelation).

V dialógovom okne si vyberieme dve premenné z ktorých chceme počítať vzájomnú koreláciu. V našom prípade je to sumárne skóre PID deliberácia a sumárne skóre PID intuícia. Ak by sme chceli korelovať viac premenných, tak ich presunieme všetky a v tom prípade bude výstupom korelačná matica. V spodnej časti sú dve zaškrtávacie políčka. Označenie jednostranného testu (one-tailed) a dvojstranného testu (Two-tailed). Ponecháme prednastavenú hodnotu two-tailed. Ďalej sa v ľavom dolnom rohu nachádza možnosť zaškrtnúť Označenie signifikatných korelácií (Flag significant correlations). Túto možnosť zaškrtneme tiež. Kliknutím OK spustíme celú analýzu.

Obr. 1. Sprievodca koreláciou

Naše výsledky:

Obr. 2 Výsledky korelačnej analýzy

Ako vidíme v tabuľke jednotlivé škály dotazníka PID spolu korelujú len slabo r = 0,25, p < 0,001.

Reportovanie výsledkov:

Reportovanie našich výsledkov: Škála PID deliberácia koreluje r = 0,25, zo škálou PID intuícia na hladine významnosti p < 0,001.

Môžeme aj kratšie: Škála PID deliberácia koreluje r = 0,25, p < 0,001, zo škálou PID intuícia.

Príklady medzinárodného (anglického) reportovania výsledkov (nesúvisia s príkladom) :

The most useful was REI-R scale that correlated with three other measures: CRT (r=0.14, p<0.01), time preference (r=0.105, p<0.05), and risk preference (r=0.115, p<0.05). (Čavojová, Hanák, 2014).

Alebo:

As we stated earlier, measures of rational thinking showed only weak correlations among themselves (CRT correlating with a composite score for risk preference, r=0.09, p=0.04 and the jelly bean task, r=0.118, p=0.007; and time preference correlating with risk preference, r=0.24, p<0.001,and Wason´s task, r=0.12, p=0.005) (Čavojová, Hanák, 2014).

Spracoval Róbert Hanák, Január 2016

Opisná štatistika

Dáta na počítanie opisnej štatistiky nájdete v súbore s názvom:

korelačná analýza

Pomocou základných štatistík ako priemer, smerodajná odchýlka a ostatné opisujeme súbor dát. Nakoľko pri akomkoľvek štatistickom skúmaní je zvykom uvádzať základné opisné štatistiky, je počítanie opisných štatistík časté. Pri publikovaní vedeckých článkov a príspevkov je vždy potrebné uvádzať priemer a smerodajnú odchýlku z našich dát, aby iní autori mohli eventuálne náš výskum zaradiť do metaanalýz. Zároveň sa opisné štatistiky vždy vyžadujú editormi vo vedeckých časopisoch alebo v iných vedeckých prácach.

Patria sem:

Priemer (Mean) je aritmetický priemer.

Smerodajná odchýlka (Standard deviaton) je štandardná smerodajná odchýlka.

Minimum (Minimum) je minimálna hodnota v súbore

Maximum (Maximum) je maximálna hodnota v súbore

Rozpätie (Range) je rozdiel medzi maximálnou a minimálnou hodnotou.

Suma (Sum) je súčet všetkých hodnôt v súbore

Štandardná chyba (Standard error) uvádza rozptýlenosť ostatných vypočítaných štatistík.

Rozptyl (Variance) je vyjadrením variability v súbore a smerodajná odchýlka je druhá odmocnina rozptylu. Čím máme v súbore dáta odlišnejšie od priemeru (moc veľké alebo moc malé), tým je rozptyl väčší.

Šikmosť (Skewness) Vyjadruje zošikmenie súboru, teda zjednodušene či prevažujú vysoké hodnoty alebo nízke hodnoty v súbore. Ak vyjde koeficient šikmosti nula, potom ide o symetrické rozdelenie. Ak je menší ako nula ide o vpravo zošikmené rozdelenie (viac väčších hodnôt a málo menších), ak je koeficient vyšší ako 0 ide o vľavo zošikmené rozdelenie (viac menších hodnôt a málo väčších).

Špicatosť (Kurtosis) Vyjadruje rozloženie dát v súbore. Ak je výsledok väčší ako 0 potom je to špicatejšie rozdelenie a ak je výsledok menší ako 0 potom je rozdelenie plochejšie. Špicaté rozdelenie prakticky znamená, že väčšina hodnôt v súbore je blízko priemeru. Plochejšie rozdelenie naopak znamená, že v súbore máme veľa nízkych aj vysokých hodnôt a nie sú blízko priemeru.

Zadanie:

Vypočítajte opisné štatistiky pre sumárnu škálu dotazníka PID deliberácia a intuícia. Tie sú v našom súbore uvedené ako posledné stĺpce vpravo a pod skratkami PID_del_total (PID škála deliberácia) a PID_In_total (PID škála intuícia).

Riešenie:

Klikneme Analyzovať (Analyze) → Opisná štatistika (Descriptives)

V ľavej časti okna sú uvedené všetky premenné v našom súbore. Vyberieme PID_del_total (PID škála deliberácia) a PID_In_total (PID škála intuícia) a presunieme ich do pravej časti s názvom Premenné (Variables) .

V dialógovom okne nám v pravej časti dole ponúka jednotlivé opisné štatistiky. Zaškrtávacím políčkom vyberiem tie, ktoré potrebujeme a následne klikneme ok a spustíme celú analýzu.

Obr. 1 Postup riešenia výpočtu opisných štatistík.

Výsledky:

Program PSPP vytvorí tabuľku s výsledkami. Dole na obrázku vidíme, že sme mali 872 prípadov a ani v jednom z nich nám nechýbali hodnoty.

Obr. 2. Výsledky riešenia opisnej štatistiky.

Interpretácia

V súbore sme mali veľkú vzorku, takže to nám dovoľuje robiť úsudky aj o celej populácii. Môžeme konštatovať, že respondenti vnímali seba samých viac deliberatívne (racionálnejšie), kde priemer M = 34,17 než intuitívne M = 30,7. Zároveň bola v jednotlivých odpovediach na otázky deliberatívnej škály väčšia variabilita o čom svedčí vyššia smerodajná odchýlka SD = 5,81 v porovnaní s intuitívnou škálou, kde SD = 5,05. Maximálnu hodnotu, ktorú mohol respondent dosiahnuť bolo 45 bodov a u obidvoch škál boli respondenti, ktorí túto hodnotu dosiahli. Čo sa týka minimálnej hodnoty, tak u škály deliberácia bola 9 bodov a u škály Intuícia 13 bodov. Špicatosť (Kurtosis) bola u škály intuícia -0,2, to je blízko 0, čo znamená, že hodnoty v súbore sú blízko normálnemu rozdeleniu v súbore. Záporné číslo znamená, že ide o plochejšie rozdelenie, teda že v súbore sú viac zastúpené skôr nižšie alebo vyššie hodnoty, než tie blízko priemeru. Naopak špicatosť (Skewness) škály deliberácia bola výrazne vyššia = 1,89, teda väčšina ľudí sa vyskytovala blízko priemeru. Šikmosť nám hovorí, či Čo sa týka šikmosti, tak v prípade deliberácie (racionality) je -1,12, teda vpravo zošikmené rozdelenie. Ľudia zaškrtali viacero vyšších hodnôt v pravej časti od priemeru. Pri intuícii je hodnota šikomosti = 0,1, teda veľmi blízka 0 a môžeme hovoriť o normálne rozložených dátach v súbore.

Reportovanie výsledkov

Vo vedeckých článkoch sa štandardne reportuje priemer spolu so smerodajnou odchýlkou. Niekedy sa uvádza minimálna aj maximálna hodnota. V našom prípade výsledky reportujeme nasledovne.

Priemerná hodnota škály deliberácie je M = 34,17; smerodajná odchýlka SD = 5,81. Minimálna hodnota Min = 9, maximálna Max = 45. Pri intuícii sme namerali nasledovné hodnoty: priemerná hodnota škály intuícia je M = 30,7; smerodajná odchýlka SD = 5,05. Minimálna hodnota Min = 13, maximálna Max = 45. Obidve škály vyplnilo 872 respondentov.

Keď sme uviedli tieto údaje potom aj iní vedci dokážu použiť tieto čísla na medzinárodné porovnávania a aj na metaanalýzy.

Reportovanie medzinárodne (V anglickom jazyku)

Príklady reportovania opisných štatistík v medzinárodnom kontexte (nesúvisia s našim príkladom):

V nasledujúcom príklade sú uvedené nielen priemery ale v zátvorkách aj variačné rozpätie a samozrejme počty respondentov podľa pohlavia.

Sixteen professional HR specialists (3 men and 13 women) with mean age 30.5 (25 – 43

years) and 16 non-experts (8 men and 8 women) with mean age 26.06 (22 – 32) participated in

the Study 2 (Čavojová, Hanák, 2014).

V druhom príklade autori uvádzajú počty respondentov ako aj priemer, variačné rozpätie a smerodajnú odchýlku.

In this experiment, 226 undergraduate Slovak students of management (148 females,

age range 18-45 years, M = 21.29, SD = 1.84) participated without incentive (Sirota, et. al. 2014).

Spracoval Róbert Hanák, November 2015