Vzťahy medzi nominálnymi premennými meriame týmito štatistickými metódami:
Koeficient phi (phi coeficient – φ)
Program PSPP má pre tento označenie PHI. Používa sa na skúmanie vzťahov medzi dvoma dichotomickými premennými, napríklad absolvoval školenie (áno = 1, nie = 0), alebo pohlavie (muž = 0, žena = 1). Výsledok výpočtu je veľmi podobný korelačnému koeficientu a nadobúda hodnoty 0 – žiadna závislosť premenných až 1 – úplná vzájomná závislosť.
Cramérovo V (Cramér’s V)
Mareš a kolektív (2015) uvádzajú, že tento koeficient sa používa na meranie vzťahov u dichotomickej premennej a premennej, ktorá nadobúda viacero kategórii než dve (napr. vzdelanie: záklané = 0, stredoškolské odborné = 1, stredoškolské s maturitou = 2, vysokoškolské bakalárske =1, atď. ). Môžeme ho použiť aj u dvoch premenných, ktoré obidve majú viac kategórií než dve. Rovnako ako u koeficientu PHI výsledok nadobúda hodnoty od 0 – žiadny vzájomný vzťah medzi premennými, až po 1 – úplný vzájomný vzťah. Softvér PSPP, nemá samostatný príkaz na výpočet, ale vypočíta Cramérovo V spolu s koeficientom PHI.
Goodmanova – Kruskalova lambda (Goodman and Kruskal’s lambda -λ)
Na rozdiel od predchádzajúcich dvoch koeficientov Goodmanova – Kruskalova lambda umožňuje merať aj predpokladaný príčinný vzťah medzi nezávislou a závislou premennou. Ak sa snažíme predpovedať jednu premennú pomocou druhej, potom lambda nám vyjadruje zníženie chyby predpovede druhej premennej ak poznáme hodnotu prvej. Ritomský a Hankes (1994, str. 138) ju definuje ako: „relatívne zníženie pravdepodobnosti chybnej predikcie jednej premennej pri znalosti hodnoty druhej premennej.“ Nadobúda hodnoty od 0 po 1. Ak nám vyjde hodnota napríklad 0,35, a toto číslo prevedieme na percentá = 35%, potom môžeme konštatovať, že sme znížili pravdepodobnosť chyby o 35%.
Koeficient Eta (Eta coeficient)
Tento koeficient meria vzťahy medzi nominálnou premennou a intervalovou. Rovnako ako hore uvedené koeficienty aj Eta nadobúda hodnoty od 0 do 1, kde hodnoty blízke nule znamenajú minimálnu, respektíve žiadnu závislosť a 1 znamená úplnú závislosť. Softvér PSPP používa skratku pre tento koeficient ETA. Rimančík (2007) uvádza, že druhá mocnina koeficientu Eta sa označuje η2 udáva aký podiel variability intervalovej premennej vysvetľuje nominálna premenná.
Príklad.
Zadanie: Zistite či existuje vzájomná závislosť medzi tým existenciou pracovnej pozície: riaditeľ informatiky a vyhodnocovaním prínosov informačných technológií.
Riešenie:
V súbore s názvom Riaditeľ IT.sav sú uvedené výsledky za 225 skutočných podnikov v SR, ktorí uviedli či majú pozíciu riaditeľa informatiky (áno = 1, nie = 0) a či a či vyhodnocujú prínosy informačných technológií (áno = 1, nie = 0). Pretože obe premenné sú dichotomické, tak musíme na vypočítanie vzájomnej súvislosti medzi nimi použiť koeficient PHI. Ďalej predpokladáme, že medzi premennými existuje príčinná súvislosť, konkrétne, že ak existuje pracovná pozícia riaditeľa informatiky, tak ten potom vyhodnocuje prínosy informačných technológií pre podnik. A preto použijeme aj Goodmanovu – Kruskalovu lambdu ako druhú štatistickú metódu na otestovanie našich hypotéz, ktoré sme si stanovili nasledovne:
H1: Pozícia riaditeľa informatiky priamo ovplyvňuje vyhodnocovanie prínosov informačných technológií.
H0: Pozícia riaditeľa informatiky neovplyvňuje vyhodnocovanie prínosov informačných technológií.
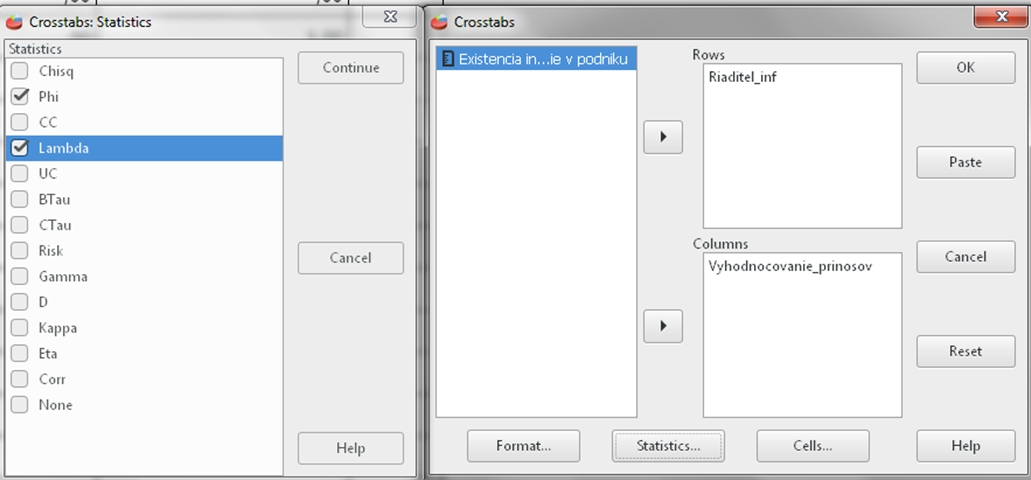
Klikneme Analyzovať (Analyze), potom Opisné štatistiky (Descriptive Statistics) a Krížové tabuľky (Crosstabs). Vyberieme nasledovné dve premenné: do okna Riadky (Rows) presunieme premennú Riaditel_inf a do okna Stĺpce (Columns) premennú Vyhodnocovanie_prinosov. V dialógovom okne si dole otvoríme Štatistisky (Statistics) a vyberieme si Koeficient Phi – Phi a Goodmanovu – Kruskalovu lambdu. Potom klikneme Ok.
Obrázok č. 1. Sprievodca pre koeficient PHI a Goodmanovu – Kruskalovu lambdou (Lambda)
Výsledok:
Obrázok č. 2. Vzájomná závislosť medzi pozíciou riaditeľa informatiky a vyhodnocovaním prínosov informačných techonológií podniku počítanej pomocou koeficientu phí (PHI) a Goodmanovou – Kruskalovou lambdou.
Interpretácia:
Koeficient fí (Phi) ako aj Cramérovo V je 0,36. Hoci koeficient nie je zanedbateľný je pomerne malý, čiže súvislosť existuje, nie je však silná. Na otestovanie hypotéz, že riaditeľ informatiky znamená následne vyhodnocovanie prínosov informačných technológií sme použili Goodmanovou – Kruskalovou lambdou kde kde λ = 0,19, p = 0,11. Hodnota Lambdy je tiež pomerne nízka a súčasne nie je štatisticky významná, nakoľko p je väčšie než hodnota 0,05. Na základe týchto výsledkov zamietame hypotézu H1 a príjmame hypotézu H0. Každopádne musíme konštatovať, že určitý vplyv tam existuje.
Reportovanie výsledkov:
Pozícia riaditeľa informatiky automaticky neznamená, že podnik bude vyhodnocovať prínosy informačných technológií. Vzájomná závislosť meraná Goodmanovou – Kruskalovou lambdou kde λ = 0,19, p = 0,11 nepreukázala štatisticky významný príčinný vzťah.
Spracoval Róbert Hanák, 13 Máj 2016