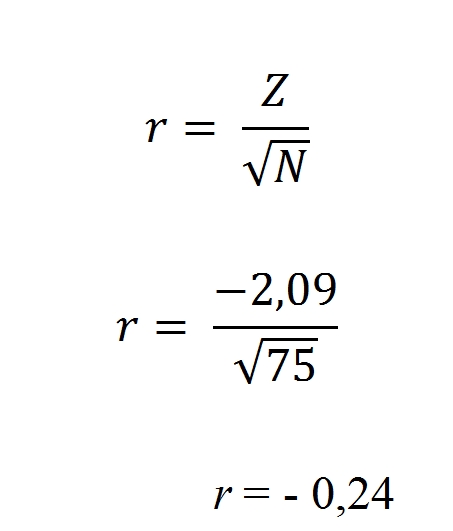Wilcoxonov test
Wilcoxonov test patrí do skupiny neparametrických testov, ktoré používame ak naše dáta nemajú normálne rozloženie. Používame ho na porovnanie rovnakej skupiny respondentov v dvoch podmienkach. Napríklad otestujeme respondentov pred experimentálnou manipuláciou a po nej a skúmame či experiment spôsobil štatisticky významne rozdielne skóre. Zjednodušene by sme mohli povedať že je ekvivalentom párového t testu.
Zadanie:
Študenti boli požiadaní aby posúdili kvalitu podnikateľského zámeru opísanú v podnikateľskom pláne a pridelili mu body (skóre) od 0 – určite skrachuje po 10 – určite bude úspešný. Plán posudzovali v dvoch podmienkach: I, v podmienke časového stresu (mali prideliť body do 3 minút od otvorenia súboru) a v II, bez časového obmedzenia. Zaujíma nás, či sa v prvom a v druhom hodnotení celkové skóre pre podnikateľský plán zmenilo. Konkrétnejšie predpokladáme, že v podmienke bez časového stresu budú hodnotiť podnikateľský plán negatívnejšie a pridelia mu menej bodov ako v časovom strese.
H1: Študenti v podmienke časového stresu ohodnotili podnikateľský plán pozitívnejšie ako v podmienke bez časového stresu.
H0: Celkové hodnotenie podnikateľského plánu sa medzi podmienkami štatisticky významne nelíši.
Riešenie:
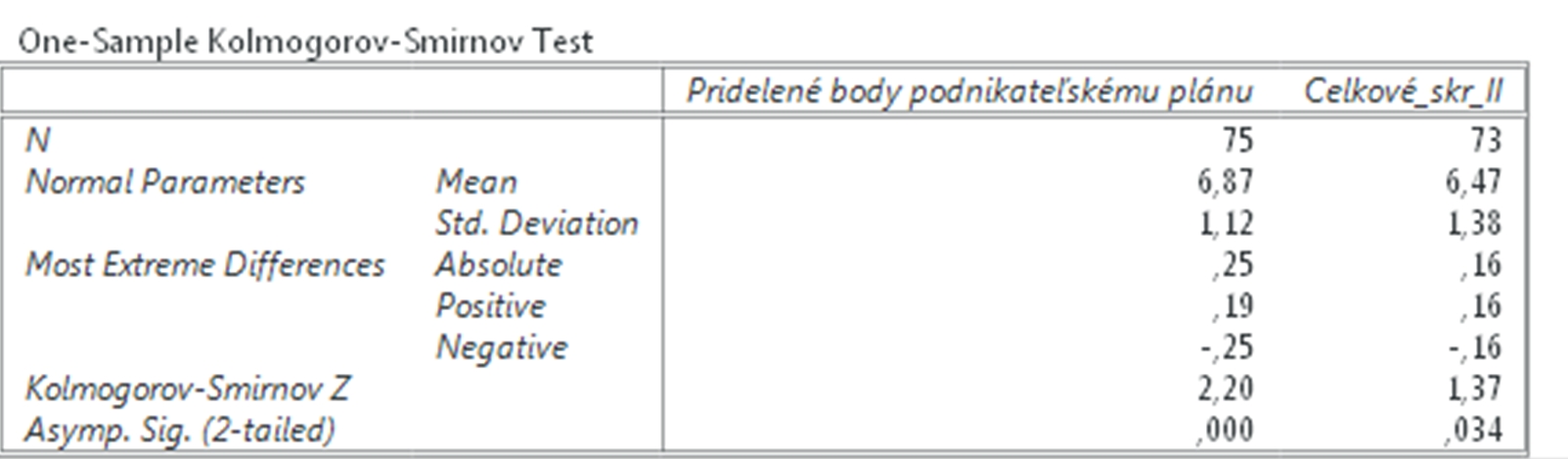
Najprv si overíme či sú naše dáta rozložené normálne. V prípade ak sú rozložené normálne, potom použijeme Párový t test a ak nie sú tak použijeme Wilcoxonov test. Výsledky Kolmogorovho – Smirnovho testu nám ukazujú, že naše dáta nie sú rozložené normálne ani pri prvej(v časovom strese) a ani pri druhej podmienke (bez časového stresu).
Obr. 1 Výsledok Kolmogorovho – Smirnovho testu.
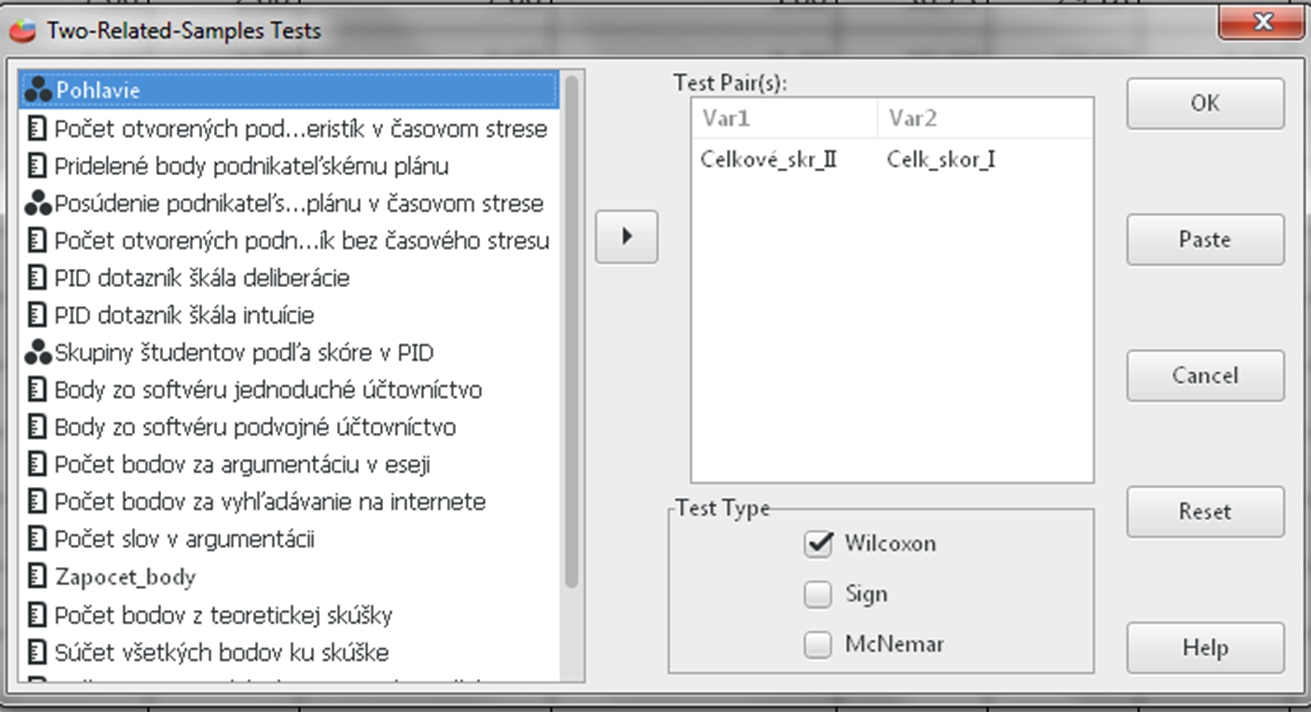
Keďže naše dáta nie sú rozložené normálne na porovnanie prvého a druhého hodnotenia použijeme Wilcoxonov test. Budeme postupovať nasledovne. Klikneme na Analyzovať (Analyze) a vyberieme si Neparametrické Štatistiky (Non-parametric statistics) a ďalej Testy pre dve súvisiace skupiny (Two – Related – Samples Tests). Následne presunieme premenné Celk_skor_I a Celkove_skr_II do okna Testované Páry (Test Pair(s)) a v spodnej časti okna zaškrtneme Wilcoxonov test (Wilcoxon). Potom klikneme Ok.
Obr. 2 Sprievdca Wilcoxonovým testom
Výsledky:
Výsledkom sú dve tabuľky. V prvej sú uvedené vzájomné vzťahy medzi jednolivými hodnoteniami. Máme 20 prípadov kedy bolo prvé hodnotenie podnikateľského plánu nižšie než druhé (Celkové_skr_II) a 33 kedy bolo prvé hodnotenie vyššie než druhé. 20 hodnotení bolo rovnakých.
Výsledky samotného Wilcoxonovho testu sú uvedené v druhej tabuľke kde Z = -2,09 na hladine významnosti p = 0,037, teda sú štatisticky významné. Na základe týchto výsledkov prijímame alternatívnu hypotézu H1.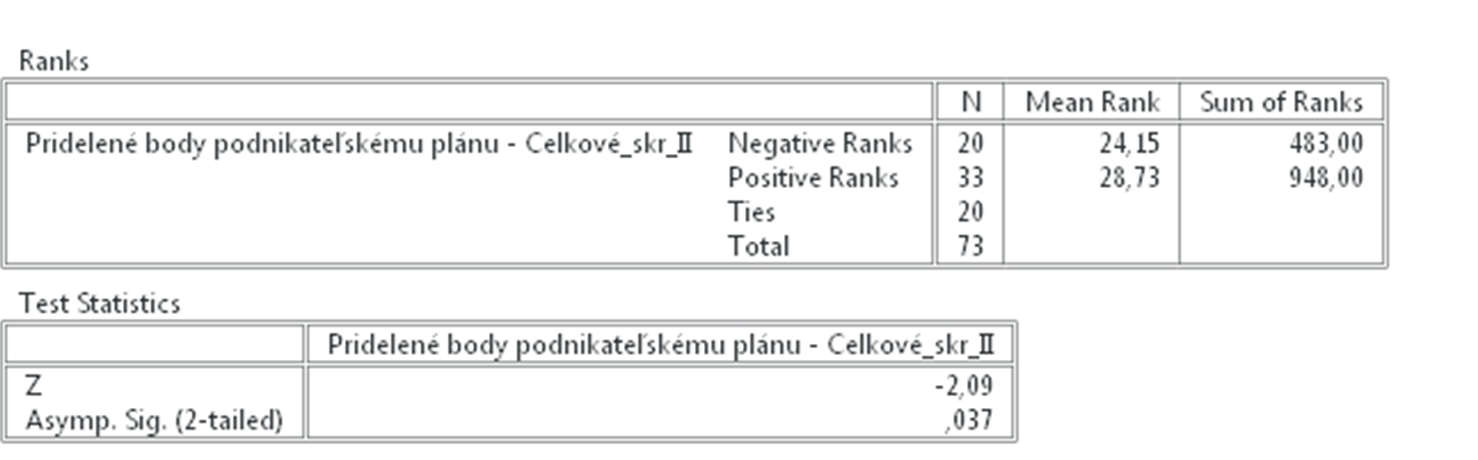
Obr. 3 Výsledok Wilcoxonovho testu
Veľkosť účinku vypočítame pre Wilcoxonov test nasledovne:
Uvádzanie výsledkov:
Respondenti ohodnotili rovnaký podnikateľský plán v podmienke časového stresu pozitívnejšie ako bez časového obmedzenia a výsledky boli štatisticky významné Z = -2,09, p = 0,037 s malým efektom účinku r = – 0,24.
Spracoval Róbert Hanák, Február 2016